【题目】如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G、E是劣弧BD上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.
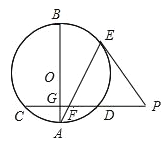
(1)求证:PE=PF
(2)已知AG=4,AF=5,EF=25,求圆O的直径.
参考答案:
【答案】(1)PE=PF;(2)圆O的直径为![]() .
.
【解析】试题分析:(1)如图1,连接OE,根据切线的性质得出∠PEO=90°,求出∠PEF=∠PFE,根据等腰三角形的判定得出即可;
(2)如图2,连接BE,根据相似三角形的判定得出△AGF∽△AEB,得出比例式,代入求出即可.
试题解析:(1)证明:如图1,连接OE,
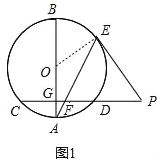
∵EP是⊙O的切线,
∴∠PEO=90°,
∴∠OEA+∠PEF=90°,
∵AB⊥CD,
∴∠AGF=90°,
∴∠A+∠AFG=90°,
∵OE=OA,
∴∠OEA=∠OAE,
∴∠PEF=∠AFG,
∵∠EFP=∠AFG,
∴∠PEF=∠PFE,
∴PE=PF;
(2)解:如图2,连接BE,
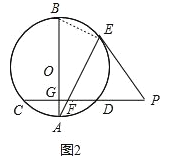
∵AB为直径,
∴∠AEB=90°,
∵∠AGF=90°,
∴∠AGF=∠AEB,
∵∠A=∠A,
∴△AGF∽△AEB,
∴![]() ,
,
∵AG=4,AF=5,EF=25,
∴![]() ,
,
∴AB=![]() ,
,
即圆O的直径为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm速度向点A运动,点Q从点A同时出发以每秒2cm速度向点C运动,其中一个动点到达端点,另一个动点也随之停止,当△APQ是以PQ为底的等腰三角形时,运动的时间是秒.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MON=30°,点A1 , A2 , A3 , …在射线ON上,点B1 , B2 , B3 , …在射线OM上,△A1B1A2 , △A2B2A3 , △A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为 .

-
科目: 来源: 题型:
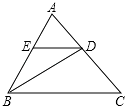
查看答案和解析>>【题目】如图所示,△ABC中,BD是∠ABC的平分线,DE∥BC,交AB于点E,∠A=60°,∠BDC=95°,求△BDE各内角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是∠AOB平分线上的点,EC⊥OA于点C,ED⊥OB于点D,连接CD,求证:
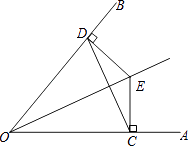
(1)∠ECD=∠EDC;
(2)OE是线段CD的垂直平分线. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE并延长AD交BE于点P;

(1)求证:AD=BE;
(2)试说明AD平分∠BAE;
(3)如图2,将△CDE绕着点C旋转一定的角度,那么AD与BE的位置关系是否发生变化,说明理由.
-
科目: 来源: 题型:
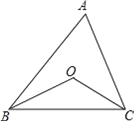
查看答案和解析>>【题目】如图,已知点O是△ABC的两条角平分线的交点,
(1)若∠A=30°,则∠BOC的大小是 ;
(2)若∠A=60°,则∠BOC的大小是 ;
(3)若∠A=n°,则∠BOC的大小是多少?试用学过的知识说明理由.
相关试题

