搜索
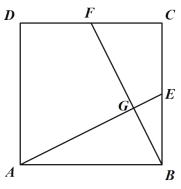
【题目】在正方形
中，
、
分别为
、
的中点，连接
、
，和交于点
．
（1）如图1，求证：
；
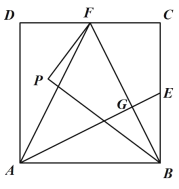
（2）如图2，作
关于对称的图形
，连接
，在不添加任何辅助线的情况下，请直接写出图2中四个三角形，使写出的每个三角形的面积都等于正方形面积的
．
参考答案：
【答案】（1）证明见解析；（2）
．
【解析】
（1）依据正方形的性质，即可得到△ABE≌△BCF（SAS），进而得出∠BAE＝∠CBF，依据∠BGE＝90
，即可得到AE⊥BF；
（2）依据E、F分别为BC、CD的中点，即可得到△ABE，△BCF，△BPF，△ADF的面积都等于正方形ABCD面积的
．
（1）证明：如图1，∵
、
分别是正方形
边
、
的中点，
∴
，
，
，
∴
∴
∴
∵
∴
∴
∴
（2）如图2，
∵E、F分别为BC、CD的中点，
S△ABE=正方形ABCD，S△BCF=正方形ABCD，S△ADF=正方形ABCD，
∵作
关于
对称的图形
∴S△BPF=S△BCF=正方形ABCD，
∴的面积都等于正方形ABCD面积的．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在 Rt△ABC 中，∠C=90°，AD 平分∠BAC 交 BC 于点 D，O 为 AB 上一点，经过点 A、D 的⊙O 分别交 AB、AC 于点 E、F，
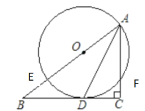
（1）求证：BC 是⊙O 切线；
（2）设 AB=m，AF=n，试用含 m、n 的代数式表示线段 AD 的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线 y x2 mx 2m 4（m>0）．
（1）证明：该抛物线与 x 轴总有两个不同的交点；
（2）设该抛物线与 x 轴的两个交点分别为 A，B（点 A 在点 B 的右侧)，与 y 轴交于点 C，A，B，三点都在圆 P 上．
①若已知 B（-3，0），抛物线上存在一点 M 使△ABM 的面积为 15，求点 M 的坐标；
②试判断：不论 m 取任何正数，圆 P 是否经过 y 轴上某个定点？若是，求出该定点的坐标，若不是，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】随着科技的进步和网络资源的丰富，在线学习已经成为更多人自主学习的选择．某校计划为学生提供以下四类在线学习方式：在线阅读、在线听课、在线答题和在线讨论．为了解学生需求，该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查，并根据调查结果绘制成如下两幅不完整的统计图．
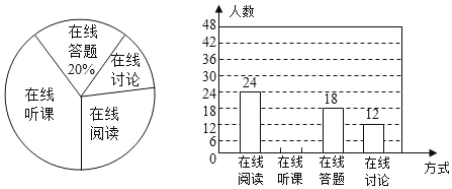
请你根据统计图中提供的信息解答下列问题：
（1）求本次调查的学生总人数；
（2）通过计算补全条形统计图；
（3）该校共有学生
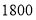人，请你估计该校对在线阅读最感兴趣的学生有多少人． -
科目： 来源： 题型：
查看答案和解析>>【题目】某交为了开展“阳光体育运动”，计划购买篮球和足球，已知足球的单价比篮球的单价多
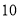元．若购买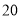
个篮球和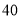
个足球需花费
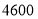元．（1）求篮球和足球的单价各是多少元；
（2）若学校购买篮球和足球共
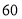个，且购买篮球的总金额不超过购买足球的总金额，则学校最多可购买多少个篮球？ -
科目： 来源： 题型：
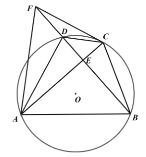
查看答案和解析>>【题目】四边形
是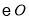
的内接四边形，
，
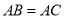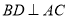，垂足为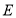
．（1）如图1，求证：
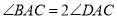；（2）如图2，点
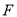在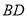
的延长线上，且
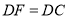，连接
、
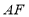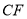，求证：
；（3）如图3，在（2）的条件下，若
，
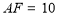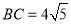，求
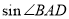的值．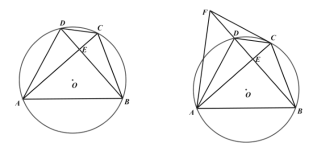
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点O为坐标原点，直线y＝﹣
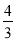x+8交x轴于点A，交y轴于点B，点C在AB上，AC＝5，CD∥OA，CD交y轴于点D．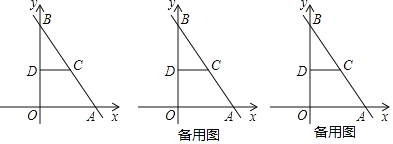
（1）求点D的坐标；
（2）点P从点O出发，以每秒1个单位长度的速度沿OA匀速运动，同时点Q从点A出发，以每秒
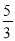个单位长度的速度沿AB匀速运动，设点P运动的时间为t秒（0＜t＜3），△PCQ的面积为S，求S与t之间的函数关系式；（3）在（2）的条件下，过点Q作RQ⊥AB交y轴于点R，连接AD，点E为AD中点，连接OE，求t为何值时，直线PR与x轴相交所成的锐角与∠OED互余．
相关试题
