【题目】随着科技的进步和网络资源的丰富,在线学习已经成为更多人自主学习的选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
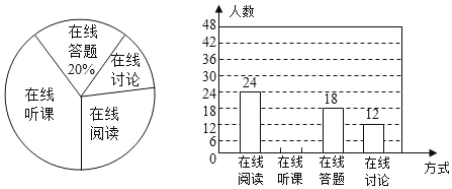
请你根据统计图中提供的信息解答下列问题:
(1)求本次调查的学生总人数;
(2)通过计算补全条形统计图;
(3)该校共有学生![]() 人,请你估计该校对在线阅读最感兴趣的学生有多少人.
人,请你估计该校对在线阅读最感兴趣的学生有多少人.
参考答案:
【答案】(1)本次调查的学生总人数为![]() 人;(2)补图见解析;(3)
人;(2)补图见解析;(3)![]() 人.
人.
【解析】
(1)用在线答题的人数除以所占的百分比即可;
(2)用总人数减去其它方式的人数,求出在线听课的人数,从而补全统计图;
(3)用该校的总人数乘以在线阅读人数所占的百分比即可.
解:(1)本次调查的学生总人数为![]() (人)
(人)
∴本次调查的学生总人数为![]() 人;
人;
(2)在线听课的人数为:![]() (人)
(人)
∴在线听课的人数为![]() 人;
人;
补全的条形统计图如图所示

(3)![]() (人)
(人)
答:估计该校对在线阅读最感兴趣的学生有![]() 人.
人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地有一个直径为 14 米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心 2 米处达到最高,高度为5米 ,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示以水平方向为 x 轴,喷水池中心为原点建立直角坐标系.
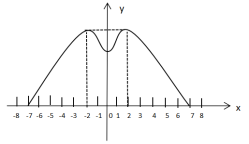
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高 1.8 米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估规划,政府决定对喷水设施改造成标志性建筑,做出如下设计改进;在喷出水柱的形状不变的前提下,把水池的直径扩大到 42 米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在 Rt△ABC 中,∠C=90°,AD 平分∠BAC 交 BC 于点 D,O 为 AB 上一点,经过点 A、D 的⊙O 分别交 AB、AC 于点 E、F,
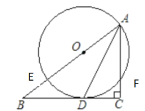
(1)求证:BC 是⊙O 切线;
(2)设 AB=m,AF=n,试用含 m、n 的代数式表示线段 AD 的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线 y x2 mx 2m 4(m>0).
(1)证明:该抛物线与 x 轴总有两个不同的交点;
(2)设该抛物线与 x 轴的两个交点分别为 A,B(点 A 在点 B 的右侧),与 y 轴交于点 C,A,B,三点都在圆 P 上.
①若已知 B(-3,0),抛物线上存在一点 M 使△ABM 的面积为 15,求点 M 的坐标;
②试判断:不论 m 取任何正数,圆 P 是否经过 y 轴上某个定点?若是,求出该定点的坐标,若不是,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形
 中,
中,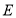 、
、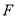 分别为
分别为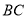 、
、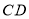 的中点,连接
的中点,连接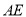 、
、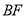 ,
,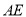 和
和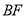 交于点
交于点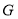 .
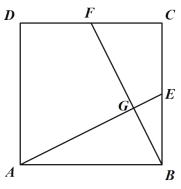
.(1)如图1,求证:
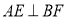 ;
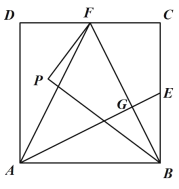
;(2)如图2,作
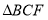 关于
关于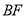 对称的图形
对称的图形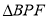 ,连接
,连接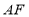 ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于正方形
,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于正方形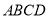 面积的
面积的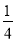 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某交为了开展“阳光体育运动”,计划购买篮球和足球,已知足球的单价比篮球的单价多
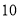 元.若购买
元.若购买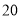 个篮球和
个篮球和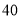 个足球需花费
个足球需花费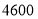 元.
元.(1)求篮球和足球的单价各是多少元;
(2)若学校购买篮球和足球共
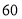 个,且购买篮球的总金额不超过购买足球的总金额,则学校最多可购买多少个篮球?
个,且购买篮球的总金额不超过购买足球的总金额,则学校最多可购买多少个篮球? -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形
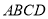 是
是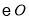 的内接四边形,
的内接四边形,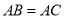 ,
,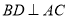 ,垂足为
,垂足为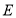 .
.(1)如图1,求证:
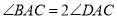 ;
;(2)如图2,点
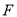 在
在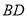 的延长线上,且
的延长线上,且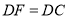 ,连接
,连接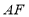 、
、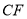 ,求证:
,求证: ;
;(3)如图3,在(2)的条件下,若
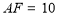 ,
,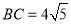 ,求
,求 的值.
的值.
相关试题

