【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣![]() x+8交x轴于点A,交y轴于点B,点C在AB上,AC=5,CD∥OA,CD交y轴于点D.
x+8交x轴于点A,交y轴于点B,点C在AB上,AC=5,CD∥OA,CD交y轴于点D.
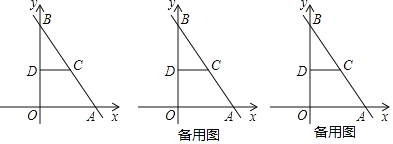
(1)求点D的坐标;
(2)点P从点O出发,以每秒1个单位长度的速度沿OA匀速运动,同时点Q从点A出发,以每秒![]() 个单位长度的速度沿AB匀速运动,设点P运动的时间为t秒(0<t<3),△PCQ的面积为S,求S与t之间的函数关系式;
个单位长度的速度沿AB匀速运动,设点P运动的时间为t秒(0<t<3),△PCQ的面积为S,求S与t之间的函数关系式;
(3)在(2)的条件下,过点Q作RQ⊥AB交y轴于点R,连接AD,点E为AD中点,连接OE,求t为何值时,直线PR与x轴相交所成的锐角与∠OED互余.
参考答案:
【答案】(1)D(0,4);(2)S=![]() t2﹣6t+12;(3)t=
t2﹣6t+12;(3)t=![]() 或
或![]()
【解析】
(1)首先证明AC=BC,利用平行线等分线段定理推出OD=BD=4即可解决问题.
(2)如图2,作PF⊥AB于点F,求出PF,CQ即可解决问题.
(3)分两种情形:当R在y轴的负半轴上,如图3中,当R在y轴的正半轴上,如图4中,用两种方法求出OR,构建方程即可解决问题.
解:(1)如图1中,
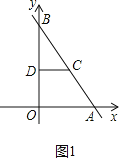
∵直线y=﹣![]() x+8交x轴于点A,交y轴于点B,
x+8交x轴于点A,交y轴于点B,
∴A(6,0),B(0,8)
∴OA=6,OB=8,
∴AB=![]() =
=![]() =10,
=10,
∵AC=5,
∴AC=BC=5,
∵CD∥OA,
∴BD=OD=4,
∴D(0,4).
(2)如图2,作PF⊥AB于点F,PA=6﹣t
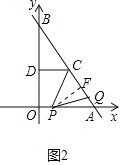
PF=PAsin∠PAF=![]() (6﹣t),
(6﹣t),
∴CQ=5﹣![]() t,
t,
S=![]() CQPF=
CQPF=![]() (5﹣
(5﹣![]() t)
t)![]() (6﹣t)=
(6﹣t)=![]() t2﹣6t+12.
t2﹣6t+12.
(3)如图3中,作OG⊥AD 于点G,
在Rt△AOD中,AD=![]() =
=![]() =2
=2![]() ,
,
∵S△AOD=![]() ODOA=
ODOA=![]() ADOG
ADOG
∴OG=![]() =
=![]() ,
,
∴DG=![]() =
=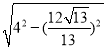 =
=![]() ,
,
∵DE=AE=![]() ,
,
∴GE=DE﹣DG=![]() ﹣
﹣![]() =
=![]() ,
,
∵∠OED+∠OPR=90°,∠OED+∠EOG=90°,
∴∠OPR=∠EOG,
∴tan∠OPR=tan∠EOG=![]()
∵BR=![]() =
= =
=![]() ﹣
﹣![]() t,
t,
∵tan∠OPR=![]() =
=![]() ,OP=t,
,OP=t,
∴OR=![]() t,
t,
当R在y轴的负半轴上,如图3中,

OR=BR﹣8=![]() ﹣
﹣![]() t,
t,
∴![]() t=
t=![]() ﹣
﹣![]() t,
t,
解得t=![]() ,
,
当R在y轴的正半轴上,如图4中,
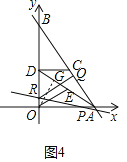
OR=8﹣BR=![]() t﹣
t﹣![]() ,
,
∴![]() t=
t=![]() t﹣
t﹣![]() ,
,
解得t=![]() ,
,
综上,当t值为![]() 或
或![]() ,直线PR与x轴相交所成的锐角与∠OED互余.
,直线PR与x轴相交所成的锐角与∠OED互余.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形
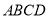 中,
中,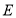 、
、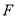 分别为
分别为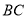 、
、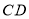 的中点,连接
的中点,连接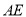 、
、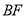 ,
,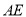 和
和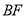 交于点
交于点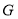 .
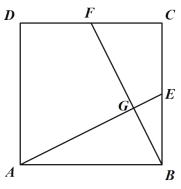
.(1)如图1,求证:
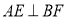 ;
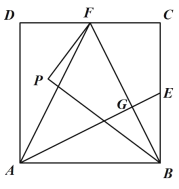
;(2)如图2,作
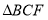 关于
关于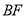 对称的图形
对称的图形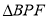 ,连接
,连接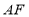 ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于正方形
,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于正方形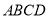 面积的
面积的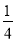 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某交为了开展“阳光体育运动”,计划购买篮球和足球,已知足球的单价比篮球的单价多
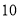 元.若购买
元.若购买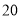 个篮球和
个篮球和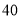 个足球需花费
个足球需花费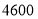 元.
元.(1)求篮球和足球的单价各是多少元;
(2)若学校购买篮球和足球共
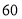 个,且购买篮球的总金额不超过购买足球的总金额,则学校最多可购买多少个篮球?
个,且购买篮球的总金额不超过购买足球的总金额,则学校最多可购买多少个篮球? -
科目: 来源: 题型:
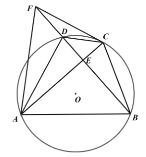
查看答案和解析>>【题目】四边形
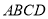 是
是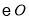 的内接四边形,
的内接四边形,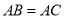 ,
,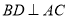 ,垂足为
,垂足为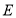 .
.(1)如图1,求证:
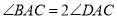 ;
;(2)如图2,点
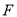 在
在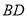 的延长线上,且
的延长线上,且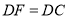 ,连接
,连接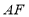 、
、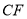 ,求证:
,求证: ;
;(3)如图3,在(2)的条件下,若
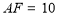 ,
,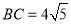 ,求
,求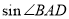 的值.
的值.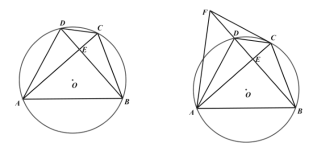
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作
 ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交
 于点M,N;
于点M,N;(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
-
科目: 来源: 题型:
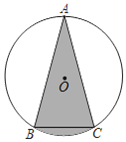
查看答案和解析>>【题目】如图,⊙O中,AB=AC,∠ACB=75°,BC=1,则阴影部分的面积是( )
A.1+
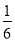 πB.
πB. πC.
πC.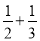 πD.1+
πD.1+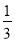 π
π -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点 A 的坐标是(﹣2,0),点 B 的坐标是(0,6),C 为 OB 的中点,将△ABC 绕点 B 逆时针旋转 90°后得到△A′B′C′.若反比例函数 y
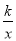 的图象恰好经过 A′B 的中点 D,则k _________.
的图象恰好经过 A′B 的中点 D,则k _________.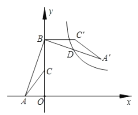
相关试题

