【题目】在△ABC中,∠ACB=2∠B,如图①,当∠C=90°,AD为∠BAC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.

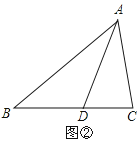

(1)如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想并证明;
(2)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.
参考答案:
【答案】(1)(2)见解析
【解析】(1)首先在AB上截取AE=AC,连接DE,易证△ADE≌△ADC(SAS),则可得∠AED=∠C,ED=CD,又由∠ACB=2∠B,易证DE=CD,则可求得AB=AC+CD;
(2)首先在BA的延长线上截取AE=AC,连接ED,易证△EAD≌△CAD,可得ED=CD,∠AED=∠ACD,又由∠ACB=2∠B,易证DE=EB,则可求得AC+AB=CD.
解:(1)猜想:AB=AC+CD.
证明:如图,在AB上截取AE=AC,连接DE,
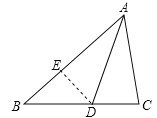
∵AD为∠BAC的角平分线时,
∴∠BAD=∠CAD,
∵AD=AD,
∴△ADE≌△ADC(SAS),
∴∠AED=∠C,ED=CD,
∵∠ACB=2∠B,
∴∠AED=2∠B,
∴∠B=∠EDB,
∴EB=ED,
∴EB=CD,
∴AB=AE+DE=AC+CD.
(2)猜想:AB+AC=CD.
证明:如图,在BA的延长线上截取AE=AC,连接ED.
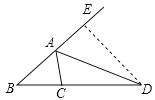
∵AD平分∠FAC,
∴∠EAD=∠CAD.
在△EAD与△CAD中,AE=AC,∠EAD=∠CAD,AD=AD,
∴△EAD≌△CAD.
∴ED=CD,∠AED=∠ACD.
∴∠FED=∠ACB.
又∠ACB=2∠B,∠FED=∠B+∠EDB,∠EDB=∠B.
∴EB=ED.
∴EA+AB=EB=ED=CD.
∴AC+AB=CD.
“点睛”此题考查了全等三角形的判定与性质以及等腰三角形的判定定理.此题难度适中,解题的关键是注意数形结合思想的应用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 正整数和负整数统称为整数; B. 最小的自然数是-1
C. 正分数和负分数统称为分数; D. a>-a
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于点O,则图中有_______对全等三角形.
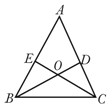
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016宁夏第20题)为了解学生的体能情况,随机选取了1000名学生进行调查,并记录了他们对长跑、短跑、跳绳、跳远四个项目的喜欢情况,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.

长跑
短跑
跳绳
跳远
200
√
×
√
√
300
×
√
×
√
150
√
√
√
×
200
√
×
√
×
150
√
×
×
×
(1)估计学生同时喜欢短跑和跳绳的概率;
(2)估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
(3)如果学生喜欢长跑、则该同学同时喜欢短跑、跳绳、跳远中哪项的可能性大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知n正整数,且x2n=2,求(3x3n)2﹣4(x2)2n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两名同学在调查观众喜欢的影片类型时使用下面提问方式,你认为哪一种更好些( )
A.难道你不认为科幻片比武打片更有意思吗?
B.你更喜欢哪一类电影--科幻片还是武打片?
C.难道你不认为武打片比科幻片更有意思吗?
D.你肯定喜欢科幻片,是吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2+8x+9=0,变形后的结果正确的是( )
A.(x+4)2=﹣7
B.(x+4)2=﹣9
C.(x+4)2=7
D.(x+4)2=25
相关试题

