【题目】如图,长方形![]() 在平面直角坐标系中,
在平面直角坐标系中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上一动点,当
上一动点,当![]() 为等腰三角形时,
为等腰三角形时,![]() 点的坐标为____________
点的坐标为____________

参考答案:
【答案】![]() ,
,![]() 或
或![]()
【解析】
由题意利用矩形性质和勾股定理求得AD的长,然后分AD=PD=5时,AD=AP=5时,AP=AD时三种情况,设P点坐标为(x,3),结合矩形性质和勾股定理求得P点坐标
解: 由题意可知:AB=OC=8,AO=BC=3
∵D为OC中点
∴OD=CD=4
∴在Rt△AOD中,![]()
当AD=PD=5时,△ADP是等腰三角形
又因为点P在线段AB上,
∴设P点坐标为(x,3),
则![]()
解得:x=0(不合题意,舍去)或x=8
∴此时P(8,3)

当AD=AP=5时,△ADP是等腰三角形
过点P作PE⊥OC,则四边形AOEP是矩形
∴此时P点坐标为(5,3)

当AP=AD时,△ADP是等腰三角形
设 P(x,3),过点P作PE⊥OC,则DE=4-x,AP=AD=x,PE=3
∴在Rt△PED中,![]()
解得:![]()
∴此时P点坐标为(![]() ,3)
,3)

综上所述,点P的坐标为![]() ,
,![]() 或
或![]() .
.
故答案为:![]() ,
,![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,直线
中,直线 经过点
经过点 ,作
,作 轴于点
轴于点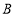 ,将
,将 绕点
绕点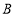 逆时针旋转
逆时针旋转 得到
得到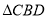 .若点
.若点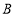 的坐标为
的坐标为 ,
, ,则点
,则点 的坐标为( )
的坐标为( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:

小亮遇到这样问题:如图1,已知AB∥CD,EOF是直线AB、CD间的一条折线.判断∠O、∠BEO、∠DFO三个角之间的数量关系.小亮通过思考发现:过点O作OP∥AB,通过构造内错角,可使问题得到解决.
请回答:∠O、∠BEO、∠DFO三个角之间的数量关系是 .
参考小亮思考问题的方法,解决问题:
(2)如图2,将△ABC沿BA方向平移到△DEF(B、D、E共线),∠B=50°,AC与DF相交于点G,GP、EP分别平分∠CGF、∠DEF相交于点P,求∠P的度数;
(3)如图3,直线m∥n,点B、F在直线m上,点E、C在直线n上,连接FE并延长至点A,连接BA、BC和CA,做∠CBF和∠CEF的平分线交于点M,若∠ADC=α,则∠M= (直接用含α的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为6的正方形
 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转 后得到正方形
后得到正方形 ,
, 交
交 于点
于点 ,则
,则 ____________.
____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=
 (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.(1)求反比例函数和直线EF的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x+b﹣
 >0的解集.
>0的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 在平面直角坐标系中的位置如图所示,先将
在平面直角坐标系中的位置如图所示,先将 向右平移3个单位,再向下平移1个单位到
向右平移3个单位,再向下平移1个单位到 ,
, 和
和 关于
关于 轴对称.
轴对称.
(1)画出
 和
和 ;
;(2)在
 轴上确定一点
轴上确定一点 ,使
,使 的值最小,试求出点
的值最小,试求出点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD,
(1)求抛物线的解析式;
(2)设点P(x,y)是第一象限内该抛物线上的一个动点,△PCD的面积为S,求S关于x的函数关系式,写出自变量x的取值范围,并求当x取多少时,S的值最大,最大是多少?

相关试题

