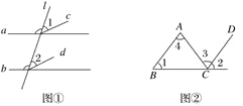
【题目】如图①所示,在直角梯形ABCD中,∠BAD=90°,E是直线AB上一点,过E作直线l∥BC,交直线CD于点F.将直线l向右平移,设平移距离BE为t(t≥0),直角梯形ABCD被直线l扫过的面积(图中阴影部分)为S,S关于t的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
信息读取
(1)梯形上底的长AB=;
(2)直角梯形ABCD的面积=;
图象理解
(3)写出图②中射线NQ表示的实际意义;
(4)当2<t<4时,求S关于t的函数关系式;
问题解决
(5)当t为何值时,直线l将直角梯形ABCD分成的两部分面积之比为1:3.
参考答案:
【答案】
(1)2
(2)12
(3)
解:当平移距离BE大于等于4时,直角梯形ABCD被直线l扫过的面积恒为12
(4)
解:当2<t<4时,如图所示,
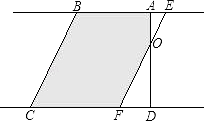
直角梯形ABCD被直线l扫过的面积S=S直角梯形ABCD﹣SRt△DOF
=12﹣ ![]() (4﹣t)×2(4﹣t)=﹣t2+8t﹣4
(4﹣t)×2(4﹣t)=﹣t2+8t﹣4
(5)
解:①当0<t<2时,有4t:(12﹣4t)=1:3,解得t= ![]() .
.
②当2<t<4时,有(﹣t2+8t﹣4):[12﹣(﹣t2+8t﹣4)]=3:1,
即t2﹣8t+13=0,
解得t=4﹣ ![]() ,t=4+
,t=4+ ![]() (舍去).
(舍去).
当t= ![]() 或t=4﹣
或t=4﹣ ![]() 时,直线l将直角梯形ABCD分成的两部分面积之比为1:3
时,直线l将直角梯形ABCD分成的两部分面积之比为1:3
【解析】解:由题意得:(1)AB=2.(2)S梯形ABCD=12.
(1)根据图②可知,当0≤t≤2时,E在线段AB上运动(包括与A、B重合),在此期间E点运动了2,因此可求得AB的长为2.(2)根据图形可知:当2<t<4时,E在AB的延长线上,且F在D点左侧,此期间E点运动了2,因此下底长为2+2=4,根据t=2时,重合部分的面积为8可求出梯形的高为4,因此梯形的面积为 ![]() ×(2+4)×4=12.(3)当t>4时,直线l与梯形没有交点,因此扫过的面积恒为梯形的面积12.(4)当2<t<4时,直线扫过梯形的部分是个五边形,如果设直线l与AD的交点为0,那么重合部分的面积可用梯形的面积减去三角形OFD的面积来求得.梯形的面积在(2)中已经求得.三角形OFD中,底边DF=4﹣t,而DF上的高,可用DF的长和∠BCD的正切值求出,由此可得出S,t的函数关系式.(5)本题要分情况讨论:①当0<t<2时,重合部分的平行四边形的面积:直角梯形AEFD的面积=1:3,据此可求出t的值.②当2<t<4时,重合部分的五边形的面积:三角形OFD的面积=3:1,由此可求出t的值.
×(2+4)×4=12.(3)当t>4时,直线l与梯形没有交点,因此扫过的面积恒为梯形的面积12.(4)当2<t<4时,直线扫过梯形的部分是个五边形,如果设直线l与AD的交点为0,那么重合部分的面积可用梯形的面积减去三角形OFD的面积来求得.梯形的面积在(2)中已经求得.三角形OFD中,底边DF=4﹣t,而DF上的高,可用DF的长和∠BCD的正切值求出,由此可得出S,t的函数关系式.(5)本题要分情况讨论:①当0<t<2时,重合部分的平行四边形的面积:直角梯形AEFD的面积=1:3,据此可求出t的值.②当2<t<4时,重合部分的五边形的面积:三角形OFD的面积=3:1,由此可求出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,若按图中规律继续下去,则∠1+∠2+…+∠n等于( )
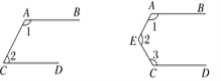

A. n·180° B. 2n·180° C. (n-1)·180° D. (n-1)2·180°
-
科目: 来源: 题型:
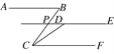
查看答案和解析>>【题目】如图,已知AB∥CF,DE∥CF,DE与BC交于点P,若∠ABC=70°,∠CDE=130°.
(1)试判断∠ABP与∠BPD之间的数量关系,并说明理由;
(2)求∠BCD的度数.
-
科目: 来源: 题型:
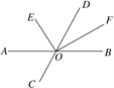
查看答案和解析>>【题目】如图,直线AB、CD交于点O,OE平分∠AOD,OF平分∠BOD.
(1)∠AOC=50°,求∠DOF与∠DOE的度数,并计算∠EOF的度数;
(2)当∠AOC的度数变化时,∠EOF的度数是否变化?若不变,求其值;若变化,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图中∠1与∠2,∠3与∠4分别是哪两条直线被哪一条直线所截而成的?是什么角?
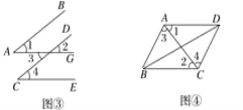
-
科目: 来源: 题型:
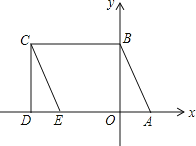
查看答案和解析>>【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(-3,2).
(1)直接写出点E的坐标;
(2)在四边形ABCD中,点P从点B出发,沿“BC→CD”移动.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①当t等于多少秒时,点P的横坐标与纵坐标互为相反数;
②求点P在运动过程中的坐标,(用含t的式子表示,写出过程);
③当3秒<t<5秒时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,用含x,y的式子表示z.
-
科目: 来源: 题型:
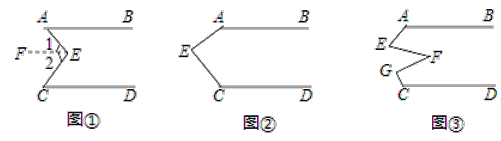
查看答案和解析>>【题目】(感知)如图①,AB∥CD,点E在直线AB与CD之间,连结AE、BE,试说明∠BEE+∠DCE=∠AEC.下面给出了这道题的解题过程,请完成下面的解题过程,并填空(理由或数学式):
解:如图①,过点E作EF∥AB
∴∠BAE=∠1( )
∵AB∥CD( )
∴CD∥EF( )
∴∠2=∠DCE
∴∠BAE+∠DCE=∠1+∠2( )
∴∠BAE+∠DCE=∠AEC
(探究)当点E在如图②的位置时,其他条件不变,试说明∠AEC+∠FGC+∠DCE=360°;
(应用)点E、F、G在直线AB与CD之间,连结AE、EF、FG和CG,其他条件不变,如图③.若∠EFG=36°,则∠BAE+∠AEF+∠FGC+∠DCG= °.
相关试题

