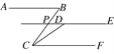
【题目】如图,已知AB∥CF,DE∥CF,DE与BC交于点P,若∠ABC=70°,∠CDE=130°.
(1)试判断∠ABP与∠BPD之间的数量关系,并说明理由;
(2)求∠BCD的度数.
参考答案:
【答案】(1)∠ABP=∠BPD,理由见解析;(2)∠BCD=20°.
【解析】
(1)根据AB∥CF,DE∥CF,可得AB∥DE,进而得出∠ABP=∠BPD;
(2)由AB∥CF,∠ABC=70°,易求∠BCF,又DE∥CF,∠CDE=130°,那么易求∠DCF,于是∠BCD=∠BCF-∠DCF可求.
(1)∠ABP=∠BPD,
理由:∵AB∥CF,DE∥CF,
∴AB∥DE,
∴∠ABP=∠BPD;
(2)∵AB∥CF,∠ABC=70°,
∴∠BCF=∠ABC=70°,
又∵DE∥CF,∠CDE=130°,
∴∠DCF+∠CDE=180°,
∴∠DCF=50°,
∴∠BCD=∠BCF-∠DCF=70°-50°=20°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.

(1)在网格的格点中,以AB为边画一个△ABC,使三角形另外两边长为
 、
、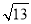 ;
;(2)若点P在图中所给网格中的格点上,△APB是等腰三角形,满足条件的点P共有 个;
(3)若将线段AB绕点A顺时针旋转90°,写出旋转后点B的坐标 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:
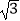 ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1: 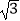 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)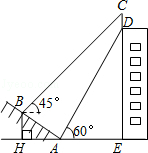
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据: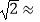 1.414,
1.414, 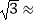 1.732)
1.732) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,若按图中规律继续下去,则∠1+∠2+…+∠n等于( )
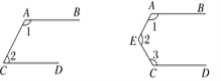

A. n·180° B. 2n·180° C. (n-1)·180° D. (n-1)2·180°
-
科目: 来源: 题型:
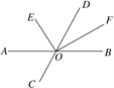
查看答案和解析>>【题目】如图,直线AB、CD交于点O,OE平分∠AOD,OF平分∠BOD.
(1)∠AOC=50°,求∠DOF与∠DOE的度数,并计算∠EOF的度数;
(2)当∠AOC的度数变化时,∠EOF的度数是否变化?若不变,求其值;若变化,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①所示,在直角梯形ABCD中,∠BAD=90°,E是直线AB上一点,过E作直线l∥BC,交直线CD于点F.将直线l向右平移,设平移距离BE为t(t≥0),直角梯形ABCD被直线l扫过的面积(图中阴影部分)为S,S关于t的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.

信息读取
(1)梯形上底的长AB=;
(2)直角梯形ABCD的面积=;
图象理解
(3)写出图②中射线NQ表示的实际意义;
(4)当2<t<4时,求S关于t的函数关系式;
问题解决
(5)当t为何值时,直线l将直角梯形ABCD分成的两部分面积之比为1:3. -
科目: 来源: 题型:
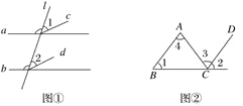
查看答案和解析>>【题目】下列图中∠1与∠2,∠3与∠4分别是哪两条直线被哪一条直线所截而成的?是什么角?
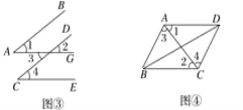
相关试题

