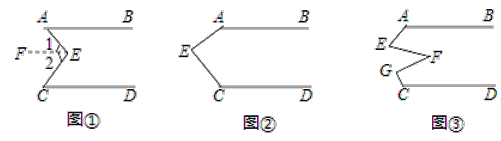
【题目】(感知)如图①,AB∥CD,点E在直线AB与CD之间,连结AE、BE,试说明∠BEE+∠DCE=∠AEC.下面给出了这道题的解题过程,请完成下面的解题过程,并填空(理由或数学式):
解:如图①,过点E作EF∥AB
∴∠BAE=∠1( )
∵AB∥CD( )
∴CD∥EF( )
∴∠2=∠DCE
∴∠BAE+∠DCE=∠1+∠2( )
∴∠BAE+∠DCE=∠AEC
(探究)当点E在如图②的位置时,其他条件不变,试说明∠AEC+∠FGC+∠DCE=360°;
(应用)点E、F、G在直线AB与CD之间,连结AE、EF、FG和CG,其他条件不变,如图③.若∠EFG=36°,则∠BAE+∠AEF+∠FGC+∠DCG= °.
参考答案:
【答案】【感知】两直线平行内错角相等,已知,平行于同一直线的两条直线平行,等式的性质;【探究】360°;【应用】396.
【解析】
在解答此题时, 过点E作EF∥AB, 由AB∥CD, 即可得AB∥EF∥CD, 然后根据两直线平行, 同旁内角互补, 即可求得答案.
解:【感知】
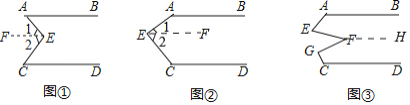
如图①,过点![]() 作
作![]()
![]() (两直线平行内错角相等)
(两直线平行内错角相等)
![]() (已知)
(已知)
![]() (平行于同一直线的两条直线平行)
(平行于同一直线的两条直线平行)
![]()
![]() (等式的性质)
(等式的性质)
![]() .
.
故答案为:两直线平行内错角相等,已知,平行于同一直线的两条直线平行,等式的性质;
【探究】
如图2中,作![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
【应用】
作![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]()
故答案为396.
-
科目: 来源: 题型:
查看答案和解析>>【题目】五一期间刚到深圳的小明在哥哥的陪伴下,打算上午从莲山春早、侨城锦绣、深南溢彩中随机选择一个景点,下午从梧桐烟云、梅沙踏浪、一街两制中随机选择一个景点,小明恰好上午选中莲山春早,下午选中梅沙踏浪的概率是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中AB=3,BC=4,∠B=90°,点B、C在两坐标轴上滑动.当边AC⊥x轴时,点A刚好在双曲线
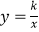 上,此时下列结论不正确的是( )
上,此时下列结论不正确的是( )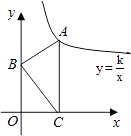
A.点B为(0,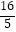 )
)
B.AC边的高为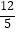
C.双曲线为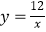
D.此时点A与点O距离最大 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )
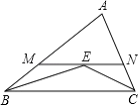
A.6
B.7
C.8
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】一名射击运动员连续打靶8次,命中的环数如图所示,则命中环数的众数与中位数分别为( )

A.9环与8环
B.8环与9环
C.8环与8.5环
D.8.5环与9环 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xOy中,A(﹣4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为( )
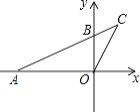
A.(1, )
)
B.( ,
,  )
)
C.(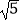 ,2
,2 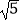 )
)
D.(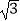 ,2
,2 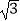 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,老师出了一道题:化简
[8(a+b)5-4(a+b)4+(-a-b)3]÷[2(a+b)3].
小明同学马上举手,下面是小明的解题过程:
[8(a+b)5-4(a+b)4+(-a-b)3]÷[2(a+b)3]
=[8(a+b)5-4(a+b)4+(a+b)3]÷8(a+b)3
=(a+b)2-
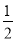 (a+b)+
(a+b)+  .
.小亮也举起了手,说小明的解题过程不对,并指了出来.老师肯定了小亮的回答.你知道小明错在哪儿吗?请指出来,并写出正确解答.
相关试题

