搜索
【题目】如图①，在△ABC中，∠BAC=90°，AB=AC，直线
经过点A，且BD⊥l于的D，CE⊥l于的E．
（1）求证：BD+CE=DE；
（2）当变换到如图②所示的位置时，试探究BD、CE、DE的数量关系，请说明理由．
参考答案：
【答案】（1）证明见解析；（2）BD-CE=DE．
【解析】
⑴证明△ABD ≌△CAE，从而得到BD=AE，AD=CE，
所以BD+CE=AE+AD=DE.
⑵证明△ABD ≌△CAE，从而得到BD=AE，AD=CE，
所以DE=AE-AD=BD-CE.
⑴∵∠DBA+∠DAB=90°，∠ DAB+∠ EAC=90°，
∴∠ DBA=∠ EAC.
在△ABD 和△CAE中，
，
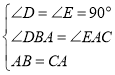∴ △ABD ≌△CAE（AAS），
∴BD=AE，AD=CE，故BD+CE=AE+AD=DE.
⑵由⑴易得，△ABD ≌△CAE，
∴BD=AE，AD=CE，故DE=AE-AD=BD-CE.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在Rt△ADE中，∠DAE=90°，C是边AE上任意一点（点C与点A、E不重合），以AC为一直角边在Rt△ADE的外部作Rt△ABC，∠BAC=90°，连接BE、CD．
（1）在图1中，若AC=AB，AE=AD，现将图1中的Rt△ADE绕着点A顺时针旋转锐角α，得到图2，那么线段BE．CD之间有怎样的关系，写出结论，并说明理由；
（2）在图1中，若CA=3，AB=5，AE=10，AD=6，将图1中的Rt△ADE绕着点A顺时针旋转锐角α，得到图3，连接BD、CE．
①求证：△ABE∽△ACD；
②计算：BD2+CE2的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图：在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连接AD、AG．
（1）求证：AD=AG；
（2）AD与AG的位置关系如何，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，CD是∠ACB的角平分线，CE是AB边上的高，
（1）若∠A=40°，∠B=60°，求∠DCE的度数．
（2）若∠A=m，∠B=n，求∠DCE．（用m、n表示）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一个质点在第一象限及x轴、y轴上运动，且每秒移动一个单位，在第1秒钟，它从原点运动到（0，1），然后接着按图中箭头所示方向运动，即（0，0）→（0，1）→（1，1）→（1，0）→…，若经过23秒质点到达点A，经过33秒质点到达点B，则直线AB的解析式为（ ）
A.y＝
x+
B.y＝﹣x+C.y＝2x+9D.y＝﹣2x+9 -
科目： 来源： 题型：
查看答案和解析>>【题目】某地下车库出口处安装了“两段式栏杆”，如图1所示，点A是栏杆转动的支点，点E是栏杆两段的联结点．当车辆经过时，栏杆AEF最多只能升起到如图2所示的位置，其示意图如图3所示（栏杆宽度忽略不计），其中AB⊥BC，EF∥BC，∠AEF=143°，AB=AE=1.2米，那么适合该地下车库的车辆限高标志牌为（ ）（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）
A．
B．
C．
D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在x轴的上方，直角∠BOA绕原点O按顺时针方向旋转，若∠BOA的两边分别与函数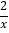y=﹣
，y=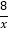
的图象交于B、A两点，则tan∠OAB的值的变化趋势为（ ）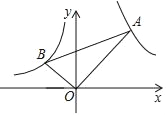
A. 逐渐变小 B. 逐渐变大 C. 时大时小 D. 保持不变
相关试题
