【题目】如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=﹣![]() ,y=
,y=![]() 的图象交于B、A两点,则tan∠OAB的值的变化趋势为( )
的图象交于B、A两点,则tan∠OAB的值的变化趋势为( )
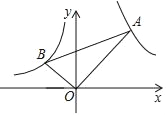
A. 逐渐变小 B. 逐渐变大 C. 时大时小 D. 保持不变
参考答案:
【答案】D
【解析】
如图,分别过点A、B作AN⊥x轴、BM⊥x轴,易证△BOM∽△OAN,根据相似三角形的性质即可得![]() ;设B(﹣m,
;设B(﹣m,![]() ),A(n,
),A(n,![]() ),则BM=
),则BM=![]() ,AN=
,AN=![]() ,OM=m,ON=n,代入即可得mn=
,OM=m,ON=n,代入即可得mn=![]() ,解得mn=4;=由△BOM∽△OAN,可得
,解得mn=4;=由△BOM∽△OAN,可得 ![]() =
=![]() =
=![]() =,由此可得tan∠OAB=
=,由此可得tan∠OAB=![]() =
=![]() 为定值,所以∠OAB的大小不变.
为定值,所以∠OAB的大小不变.
如图,分别过点A、B作AN⊥x轴、BM⊥x轴;

∵∠AOB=90°,
∴∠BOM+∠AON=∠AON+∠OAN=90°,
∴∠BOM=∠OAN,
∵∠BMO=∠ANO=90°,
∴△BOM∽△OAN,
∴![]() ;
;
设B(﹣m,![]() ),A(n,
),A(n,![]() ),
),
则BM=![]() ,AN=
,AN=![]() ,OM=m,ON=n,
,OM=m,ON=n,
∴mn=![]() ,mn=
,mn=![]() =4;
=4;
∵∠AOB=90°,
∴tan∠OAB=![]() ①;
①;
∵△BOM∽△OAN,
∴![]() =
=![]() =
=![]() ②,
②,
由①②知tan∠OAB=![]() 为定值,
为定值,
∴∠OAB的大小不变.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,直线
 经过点A,且BD⊥l于的D,CE⊥l于的E.
经过点A,且BD⊥l于的D,CE⊥l于的E.(1)求证:BD+CE=DE;
(2)当变换到如图②所示的位置时,试探究BD、CE、DE的数量关系,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个质点在第一象限及x轴、y轴上运动,且每秒移动一个单位,在第1秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→…,若经过23秒质点到达点A,经过33秒质点到达点B,则直线AB的解析式为( )

A.y=
 x+
x+ B.y=﹣
B.y=﹣ x+
x+ C.y=2x+9D.y=﹣2x+9
C.y=2x+9D.y=﹣2x+9 -
科目: 来源: 题型:
查看答案和解析>>【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=
 x+6与x轴,y轴相交于点A,B,点C在线段OA上,将△BOC沿着BC折叠后,点O恰好落在AB边上的点D处,若点P为平面内异于点C的一点,且满足△ABC与△ABP全等,则点P的坐标为_____.
x+6与x轴,y轴相交于点A,B,点C在线段OA上,将△BOC沿着BC折叠后,点O恰好落在AB边上的点D处,若点P为平面内异于点C的一点,且满足△ABC与△ABP全等,则点P的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校决定在4月7日开展“世界无烟日”宣传活动,活动有A.社区板报、B.集会演讲、C.喇叭广播、D.发宣传画四种宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了如下两种不完整的统计图表:

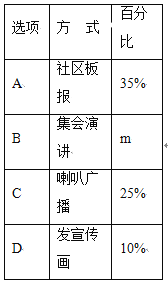
请结合统计图表,回答下列问题:
(1)本次抽查的学生共______人,m=____________,并将条形统计图补充完整;
(2)若该校学生有1500人,请你估计该校喜欢“集会演讲”这项宣传方式的学生约有多少人?
(3)学校采用抽签方式让每班在A、B、C、D四种宣传方式中随机抽取两种进行展示,请用树状图或列表法求某班所抽到的两种方式恰好是“集会演讲”和“喇叭广播”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.

相关试题

