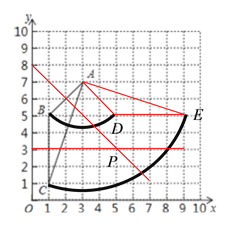
【题目】如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.建立如图所示的直角坐标系,
请在图中标出△ABC的外接圆的圆心P的位置,并填写: 圆心P的坐标:P( , )
(2)将△ABC绕点A逆时针旋转90°得到△ADE,画出图
形,并求△ABC扫过的图形的面积.

参考答案:
【答案】(1)P( 5 , 3 ) (2)![]()
【解析】试题分析:
(1)由外心是三角形各边垂直平分线的交点可知,我们在方格纸中画出AB和BC两边的垂直平分线就可找到外心,并得到其坐标;
(2)如图,在旋转过程中,△ABC扫过的面积=S扇形ACE+S△ABC,因此我们只需要利用图中的信息由勾股定理计算出AC的长就可计算了.
试题解析:
(1)如图,利用图中的格点分别画出线段AB和BC的垂直平分线,两条垂直平分线的交点为所求的P点,由图可得点P的坐标为(5,3);
(2)根据图中信息由勾股定理可得: ![]() ,∴△ABC在旋转过程中扫过的面积为:S扇形ACE+S△ABC=
,∴△ABC在旋转过程中扫过的面积为:S扇形ACE+S△ABC=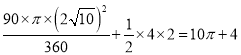 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点。
(1)求抛物线的解析式。
(2)求△ABC的面积。若P是抛物线上一点(异于点C),且满足△ABP的面积等于△ABC的面积,求满足条件的点P的坐标。
(3)点M是线段BC上的点(不与B,C重合),过M作MN∥
 轴交抛物线于N,若点M的横坐标为
轴交抛物线于N,若点M的横坐标为 ,请用含
,请用含 的代数式表示线段MN的长。
的代数式表示线段MN的长。(4)在(3)的条件下,连接NB、NC,则是否存在点M,使△BNC的面积最大?若存在,求
 的值,并求出△BNC面积的最大值。若不存在,说明理由。
的值,并求出△BNC面积的最大值。若不存在,说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)(-3x2y)(4x-3xy2-1); (2)(1-3y)(1+3y)(1+9y2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一个底角比顶角大30°,那么顶角度数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点 P(2,3)与点 Q 关于 y 轴对称,则 Q点坐标为________
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 哥哥的身高比弟弟高是必然事件
B. 今年的12月1日有雨是不确定事件
C. 随机掷一枚均匀的硬币两次,都是正面朝上是不可能事件
D. “彩票中奖的概率为
 ”表示买5张彩票肯定会中奖
”表示买5张彩票肯定会中奖 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )

A. ②④⑤⑥ B. ①③⑤⑥ C. ②③④⑥ D. ①③④⑤
相关试题

