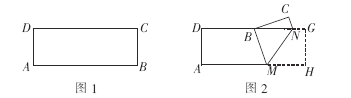
【题目】如图1,2在矩形纸片ABCD中,AD=6,AB=9.点M,N分别在AB,DC上(M不与A,B重合,N不与C,D重合),现以MN为折痕,将矩形纸片ABCD折叠.
(1)当B 点落在DC上时(如图2),求证:△MNB是等腰三角形;
(2)当B点与D点重合时,试求△MNB的面积;
(3)当B点与AD的中点重合时,试求折痕MN的长.
参考答案:
【答案】(1)证明见解析;(2)S△MNB=19.5;(3)MN=2![]() .
.
【解析】试题分析:(1)先判断出AM∥DN,进而得出∠BNM=∠BMN=∠NMH,即可得出结论;
(2)先根据勾股定理求出DN,再用三角形得面积公式即可得出结论;
(3)先根据勾股定理求出BH,再判断出△ABH∽△EMN即可得出结论.
试题解析:(1)如答图1,
∵四边形AHGD是矩形 ,
∴AM∥DN,
∴∠BNM=∠BMN=∠MNH,
∴△MNB是等腰三角形.;
(2)如答图2,当点B与点D重合时,
设MB=MF=x,则AM=9-x,
由勾股定理得:62+(9-x)2=x2,解得x=6.5,
∴MD=ND=6.5,
∴S△MNB=![]() ×6×6.5=19.5.
×6×6.5=19.5.
(3)如答图3,当点B与AD的中点重合时,连接BH交MN于点F,过点N作NE⊥AH于点E,
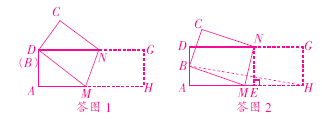
∵AD=6,
∴AB=DB=3,
∴BH2=32+92.
∴BH=3![]() .
.
∵NM垂直平分HB,NE⊥AH,
∴∠MNE=∠AHB.
∵∠A=∠NEM,
∴△ABH~△AHB.
∴![]() .
.
∴![]() .
.
∴MN=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OP1A1B1,A1P2A2B2,A2P3A3B3,……,An-1PnAnBn都是正方形,对角线OA1,A1A2,A2A3,……,An-1An都在y轴上(n≥1的整数),点P1(x1,y1),P2(x2,y2),……,Pn(xn,yn)在反比例函数y=
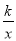 (x>0)的图象上,并已知B1(-1,1).
(x>0)的图象上,并已知B1(-1,1).
(1)求反比例函数y=
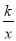 的解析式;
的解析式;(2)求点P2和P3的坐标;
(3)由(1)、(2)的结果或规律试猜想并直接写出:△PnBnO的面积为 ,点Pn的坐标为______(用含n的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上有三个点
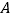 、
、 、
、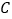 ,如图所示.
,如图所示.
(1)将点
 向左平移4个单位,此时该点表示的数是________;
向左平移4个单位,此时该点表示的数是________; (2)将点
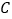 向左平移3个单位得到数
向左平移3个单位得到数 ,再向右平移2个单位得到数
,再向右平移2个单位得到数 ,则
,则 ,
, 分别是多少?
分别是多少? (3)怎样移动
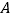 、
、 、
、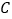 中的两点,使三个点表示的数相同?你有几种方法?
中的两点,使三个点表示的数相同?你有几种方法? -
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上从左到右的三个点
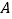 ,
,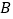 ,
,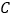 所对应的数分别为
所对应的数分别为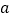 ,
,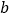 ,
,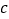 .其中
.其中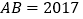 ,
,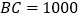 ,如图所示.
,如图所示.
(1)若以
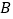 为原点,写出点
为原点,写出点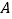 ,
,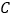 所对应的数,并计算
所对应的数,并计算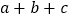 的值.
的值. (2)若原点
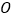 在
在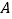 ,
,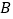 两点之间,求
两点之间,求 的值.
的值. (3)若
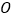 是原点,且
是原点,且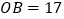 ,求
,求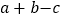 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】张新是某县城中学的在校住宿生,开学初父母通过估算为他预存了一个学期的伙食费1600元,学校的学生食堂规定一天的伙食标准:早餐每人4元,中餐、晚餐只能各选一份价格如下表中的饭菜.
(1)请问该校每位住宿生一天的伙食费有几种可能的价格?其金额各是多少元?
(2)若张新选择(1)中一天的伙食费的两种价格,并计划用膳110天,且刚好用完预存款,那么他应有哪几种选择价格的方案?每种方案中两种价格各用膳多少天?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市自来水公司为限制单位用水,每月只给某单位计划内用水 3000 吨,计划内用水每吨收费 0.5元,超计划部分每吨按 0.8 元收费.
(1)写出该单位水费 y(元)与每月用水量 x(吨)之间的函数关系式:(写出自变量取值范围)
①用水量小于等于 3000 吨 ;
②用水量大于 3000 吨 .
(2)某月该单位用水 3200 吨,水费是 元;若用水 2800 吨,水费 元.
(3)若某月该单位缴纳水费 1580 元,则该单位用水多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某检修小组乘汽车从
 地出发,在东西走向的马路上检修线路,如果规定向东行驶为正,一天中七个检修点的行驶记录如下(单位:
地出发,在东西走向的马路上检修线路,如果规定向东行驶为正,一天中七个检修点的行驶记录如下(单位: ):
):-4,+7,-9,+8,+6,-4,-3.
(1)收工时汽车共行驶了多少千米?
(2)收工时,汽车距
 地多远?
地多远? (3)在检修时,第几个检修点离
 地最远,最远距离是多少?
地最远,最远距离是多少?
相关试题

