【题目】如图,四边形OP1A1B1,A1P2A2B2,A2P3A3B3,……,An-1PnAnBn都是正方形,对角线OA1,A1A2,A2A3,……,An-1An都在y轴上(n≥1的整数),点P1(x1,y1),P2(x2,y2),……,Pn(xn,yn)在反比例函数y=![]() (x>0)的图象上,并已知B1(-1,1).
(x>0)的图象上,并已知B1(-1,1).

(1)求反比例函数y=![]() 的解析式;
的解析式;
(2)求点P2和P3的坐标;
(3)由(1)、(2)的结果或规律试猜想并直接写出:△PnBnO的面积为 ,点Pn的坐标为______(用含n的式子表示).
参考答案:
【答案】(1)反比例函数的解析式为y=![]() ;(2)点P3的坐标为(
;(2)点P3的坐标为(![]() -
-![]() ,
, ![]() +
+![]() );(3)1,(
);(3)1,( ![]() -
-![]() ,
, ![]() +
+![]() )
)
【解析】试题分析:(1)由四边形OP1A1B1为正方形且OA1是对角线知B1与P1关于y轴对称,得出点P1(1,1),据此可得答案;
(2)连接P2B2、P3B3,分别交y轴于点E、F,由点P1坐标及正方形的性质知OA1=2,据此可设P2的坐标为(a,a+2),代入解析式求得a的值即可,同理可得点P3的坐标;
(3)由S△P1B1O=2S△P1CO=2×![]() =1,S△P2B2O=2S△P2EO=2×
=1,S△P2B2O=2S△P2EO=2×![]() =1可知△PnBnO的面积为1,根据P1(1,1)、P2(
=1可知△PnBnO的面积为1,根据P1(1,1)、P2(![]() -1,
-1, ![]() +1)、P3(
+1)、P3(![]() -
-![]() ,
, ![]() +
+![]() )知点Pn的坐标为(
)知点Pn的坐标为(![]() -
-![]() ,
, ![]() +
+![]() ).
).
试题解析:(1)在正方形OP1A1B1中,OA1是对角线,则B1与P1关于y轴对称,又B1(-1,1),
∴P1(1,1),k=1.
∴反比例函数的解析式为y=![]() .
.
(2)连接P2B2,P3B3分别交y轴于点E,点F,又点P1(1,1),
∴OA1=2,设点P2的坐标为(a,a+2),将点P2(a,a+2)代入y=![]() (x>0),可得a=
(x>0),可得a=![]() -1,故点P2的坐标为(
-1,故点P2的坐标为(![]() -1,
-1, ![]() +1);(4分)
+1);(4分)
则A1E=A2E=2![]() -2,OA2=OA1+A1A2=2
-2,OA2=OA1+A1A2=2![]() ,
,
设点P3的坐标为(b,b+2 ![]() ),将P3的坐标(b,b+2
),将P3的坐标(b,b+2 ![]() )代入y=
)代入y=![]() (x>0),可得b=
(x>0),可得b=![]() -
-![]() ,故点P3的坐标为(
,故点P3的坐标为(![]() -
-![]() ,
, ![]() +
+![]() );
);
(3)∵S△P1B1O=2S△P1CO=2×![]() =1,S△P2B2O=2S△PaEO=2×
=1,S△P2B2O=2S△PaEO=2×![]() =1,…
=1,…
∴△PnBnO的面积为1,
由P1(1,1)、P2(![]() 1,
1, ![]() +1)、P3(
+1)、P3(![]()
![]() +
+![]() )知点Pn的坐标为(
)知点Pn的坐标为(![]() -
-![]() ,
, ![]() +
+![]() )
)
故答案为:1,( ![]() -
-![]() ,
, ![]() +
+![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知王亮家、公园、新华书店在一条直线上,下面的图象反映的过程是:王亮从家跑步去公园,在那里锻炼了一阵后又走到新华书店去买书,然后散步走回家.其中
 表示时间,
表示时间, 表示王亮离家的距离.
表示王亮离家的距离.
根据图象回答:
(1)公园离王亮家
 ,王亮从家到公园用了
,王亮从家到公园用了  ;
;(2)公园离新华书店
 ;
;(3)王亮在新华书店逗留了
 ;
;(4)王亮从新华书店回家的平均速度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形.
(2)若AB=5,BD=8,求矩形AODE的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】从背面相同的同一副扑克牌中取出红桃9张、黑桃10张、方块11张,现将这些牌洗匀背面朝上放在桌面上.
(1)求从中抽出一张牌是红桃的概率;
(2)现从桌面上先抽掉若干张黑桃,再放入与抽掉的黑桃张数相同的红桃,并洗匀且背面都朝上排开后,随机抽一张是红桃的概率不小于
 ,问至少抽掉了多少张黑桃?
,问至少抽掉了多少张黑桃?(3)若先从桌面上抽掉9张红桃和m(m>6)张黑桃后,再在桌面抽出一张牌.
①当m为何值时,事件“再抽出的这张牌是方块”为必然事件?
②当m为何值时,事件“再抽出的这张牌是方块”为随机事件?并求出这个事件的概率的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上有三个点
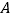 、
、 、
、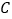 ,如图所示.
,如图所示.
(1)将点
 向左平移4个单位,此时该点表示的数是________;
向左平移4个单位,此时该点表示的数是________; (2)将点
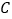 向左平移3个单位得到数
向左平移3个单位得到数 ,再向右平移2个单位得到数
,再向右平移2个单位得到数 ,则
,则 ,
, 分别是多少?
分别是多少? (3)怎样移动
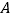 、
、 、
、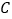 中的两点,使三个点表示的数相同?你有几种方法?
中的两点,使三个点表示的数相同?你有几种方法? -
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上从左到右的三个点
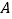 ,
,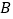 ,
,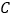 所对应的数分别为
所对应的数分别为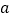 ,
,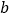 ,
,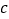 .其中
.其中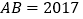 ,
,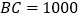 ,如图所示.
,如图所示.
(1)若以
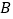 为原点,写出点
为原点,写出点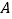 ,
,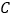 所对应的数,并计算
所对应的数,并计算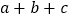 的值.
的值. (2)若原点
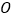 在
在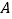 ,
,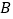 两点之间,求
两点之间,求 的值.
的值. (3)若
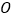 是原点,且
是原点,且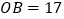 ,求
,求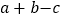 的值.
的值. -
科目: 来源: 题型:
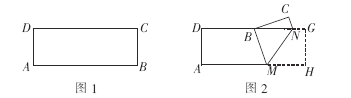
查看答案和解析>>【题目】如图1,2在矩形纸片ABCD中,AD=6,AB=9.点M,N分别在AB,DC上(M不与A,B重合,N不与C,D重合),现以MN为折痕,将矩形纸片ABCD折叠.
(1)当B 点落在DC上时(如图2),求证:△MNB是等腰三角形;
(2)当B点与D点重合时,试求△MNB的面积;
(3)当B点与AD的中点重合时,试求折痕MN的长.
相关试题

