【题目】如图,四边形ABCD是菱形,对角线AC、BD相交于点O,分别延长OB,OD到点E,F,使BE=DF,顺次连接A、E、C、F各点. 
(1)求证:∠FAD=∠EAB.
(2)若∠ADC=130°,要使四边形AECF是正方形,求∠FAD的度数.
参考答案:
【答案】
(1)证明:∵菱形ABCD的对角线AC,BD相交于点O,
∴AD=AB,∠ADB=∠ABD,
∴∠ADF=∠ABE,
在△FAD与△EAB中,
∴△FAD≌△EAB(SAS),
∴∠FAD=∠EAB;
(2)解:∵四边形AECF对角线互相垂直平分,
∴只要∠EAF=90°即得四边形BFDE是正方形,
∵∠ADC=130°,
∴∠DAB=180°﹣130°=50°
∴∠FAD+∠EAB=40°,
∵∠FAD=∠EAB,
∴∠FAD= ![]() ×40°=20°.
×40°=20°.
【解析】(1)由题意易证∠ADF=∠ABE,又因为DF=EB,AD=AB,于是可△FAD≌△EAB,;(2)由已知可得四边形AECF对角线互相垂直平分,只要∠EAF=90°即得四边形AECF是正方形,由∠FAD=∠EAB,再证得∠DAB=50°,可得∠FAD+∠EAB=40°,于是∠FAD= ![]() ×40°=20°.
×40°=20°.
【考点精析】本题主要考查了菱形的性质和正方形的判定方法的相关知识点,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中,正确的是( )
A.a2+a3=a5B.a2a3=a6
C.(a3b2)3=a6b5D.(a2)5=(﹣a5)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】若 (x+3)(x+m)=x2-2x-15,则 m 的值为( )
A. 5 B. -5 C. 2 D. -2
-
科目: 来源: 题型:
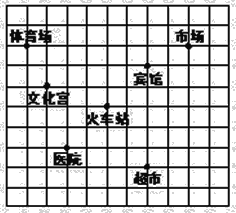
查看答案和解析>>【题目】如图,这是某市部分简图,为了确定各建筑物的位置:
(1)请你以火车站为原点建立平面直角坐标系﹒
(2)写出超市的坐标(小正方形网格的单位长度为1)﹒
(3)请将体育场、宾馆和火车站看作三点,用线段连接起来,得到三角形ABC,然后将此三角形向下平移4个单位,再画出平移后的三角形A′B′C′,并计算三角形A′B′C′的面积﹒
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小红两人周末去爬山,小红先出发,中间休息了一段时间,然后按休息前的进度继续前进,最后比小明迟到达山顶.设他们俩从山脚出发后所用的时间t(分钟)与所走的路程S(米)之间的函数关系如图所示:

(1)根据图象小明登山的速度为米/分,小红的登山速度为米/分.
(2)求出BC段图象的函数关系式,并写出自变量的取值范围.
(3)小明到达山顶后,小红还有多少米到山顶? -
科目: 来源: 题型:
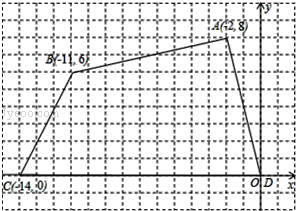
查看答案和解析>>【题目】如图,有一块不规则的四边形图形ABCD,各个顶点的坐标分别为A(﹣2,8),B(﹣11,6),C(﹣14,0),D(0,0),
(1)确定这个四边形的面积
(2)如果把原来四边形ABCD的各个顶点的纵坐标保持不变,横坐标加1,画出平移后的图形。
(3)求出平移后四边形面积
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC为矩形,A点在x轴上,C点在y轴上,矩形一角经过翻折后,顶点B落在OA边的点G处,折痕为EF,F点的坐标是(4,1),∠FGA=30°.
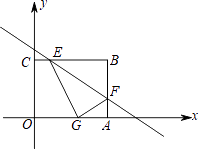
(1)求B点坐标.
(2)求直线EF解析式.
(3)若点M在y轴上,直线EF上是否存在点N,使以M、N、F、G为顶点的四边形是平行四边形?若存在,求N点的坐标;若不存在,请说明理由.
相关试题

