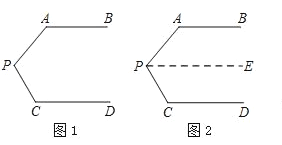
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
小明的解题思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?请说明理由;
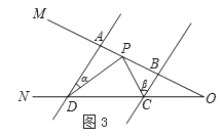
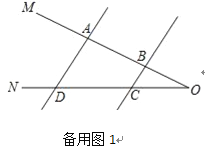
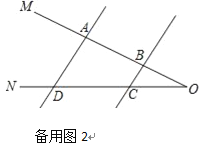
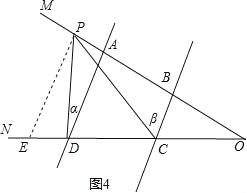
(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.
参考答案:
【答案】(1)∠CPD=∠α+∠β,理由见解析;
(2)当P在BA延长线时,∠CPD=∠β﹣∠α;当P在AB延长线时,∠CPD=∠α﹣∠β.
【解析】试题分析:(1)、首先过P作PE∥AD交CD于E,然后根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,从而得出所求的答案;(2)、根据第一题同样的方法得出角度之间的关系,从而得出答案.
试题解析:(1)解:∠CPD=∠α+∠β,理由如下:
如图3,过P作PE∥AD交CD于E,
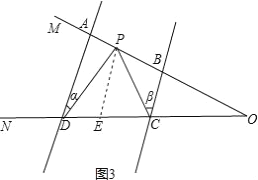
∵AD∥BC, ∴AD∥PE∥BC, ∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
(2)当P在BA延长线时,∠CPD=∠β﹣∠α;
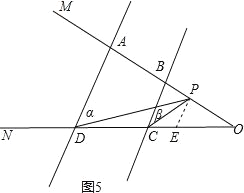
当P在AB延长线时, ∠CPD=∠α﹣∠β.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2y+2xy2+y3=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个数的立方等于它本身,这个数是_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两台机器共加工一批零件,在加工过程中两台机器均改变了一次工作效率.从工作开始到加工完这批零件两台机器恰好同时工作6小时.甲、乙两台机器各自加工的零件个数y(个)与加工时间x(时)之间的函数图象分别为折线OA﹣AB与折线OC﹣CD.如图所示.
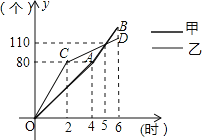
(1)甲机器改变工作效率前每小时加工零件 个.
(2)求乙机器改变工作效率后y与x之间的函数关系式,并求出自变量x的取值范围.
(3)求这批零件的总个数.
(4)直接写出当甲、乙两台机器所加工零件数相差10个时,x的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的解题过程,并在横线上补全推理过程或依据.
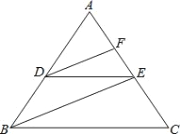
已知:如图, DE∥BC,DF、BE分别平分∠ADE、∠ABC.试说明∠FDE=∠DEB.
解:∵DE∥BC(已知)
∴∠ADE= .( )
∵DF、BE分别平分∠ADE、∠ABC (已知)
∴∠ADF=
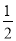 ∠ADE
∠ADE∠ABE=
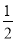 ∠ABC(角平分线定义)
∠ABC(角平分线定义)∴∠ADF=∠ABE( )
∴DF∥ .( )
∴∠FDE=∠DEB.( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】楚天汽车销售公司5月份销售某种型号汽车,当月该型号汽车的进价为30万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.
(1)设当月该型号汽车的销售量为x辆(x≤30,且x为正整数),实际进价为y万元/辆,求y与x的函数关系式;
(2)已知该型号汽车的销售价为32万元/辆,公司计划当月销售利润25万元,那么该月需售出多少辆汽车?(注:销售利润=销售价﹣进价)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣10+(+6)-(-2)=______
相关试题

