【题目】已知,△ABC中,∠ACB=90°,AC=BC,点D为BC边上的一点.
(1)以点C为旋转中心,将△ACD逆时针旋转90°,得到△BCE,请你画出旋转后的图形;
(2)延长AD交BE于点F,求证:AF⊥BE;
(3)若AC=![]() ,BF=1,连接CF,则CF的长度为______.
,BF=1,连接CF,则CF的长度为______.

参考答案:
【答案】(1)答案见解析;(2)答案见解析;(3)![]() .
.
【解析】试题分析:(1)根据题意补全图形;
(2)由旋转的性质得到∠CBE=∠CAD,∠BCE=∠ACD=90°,进而得到∠CAD+∠E=90°,即可的得到结论;
(3)易证△ADC∽△BDF,△ADB∽△CDF,由相似三角形的性质即可得到结论.
试题解析:解:(1)补全图形如下:
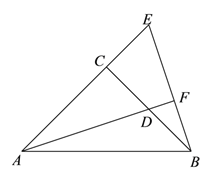
(2)证明:∵ΔCBE由ΔCAD旋转得到,∴ΔCBE≌ΔCAD,∴∠CBE=∠CAD,∠BCE=∠ACD=90°,∴∠CBE+∠E=∠CAD+∠E,∴∠BCE=∠AFE=90°,∴AF⊥BE.
(3)∵∠ACB=∠DFB=90°,∠CDA=∠FDB,∴△ADC∽△BDF,∴ ![]() ,∴
,∴![]() .∵∠ADB=∠CDF,∴△ADB∽△CDF,∴
.∵∠ADB=∠CDF,∴△ADB∽△CDF,∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴CF=
,∴CF=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C、F为⊙O上两点,且点C为弧BF的中点,过点C作AF的垂线,交AF的延长线于点E,交AB的延长线于点D.
(1)求证:DE是⊙O的切线;
(2)如果半径的长为3,tanD=
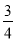 ,求AE的长.
,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明根据学习函数的经验,对函数
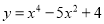 的图象与性质进行了探究.
的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组对应数值如下表:

其中m=__________;
(2)如图,在平面直角坐标系xOy中,描出了以上表中各组对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)观察函数图象,写出一条该函数的性质;
(4)进一步探究函数图象发现:
①方程
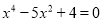 有个互不相等的实数根;
有个互不相等的实数根;②有两个点(x1,y1)和(x2,y2)在此函数图象上,当x2>x1>2时,比较y1和y2的大小关系为:
y1________y2 (填“>”、“<”或“=”);
③若关于x的方程
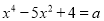 有4个互不相等的实数根,则a的取值范围是________.
有4个互不相等的实数根,则a的取值范围是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=mx2-2mx-3 (m≠0)与y轴交于点A,其对称轴与x轴交于点B顶点为C点.
(1)求点A和点B的坐标;
(2)若∠ACB=45°,求此抛物线的表达式;
(3)在(2)的条件下,垂直于
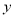 轴的直线
轴的直线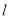 与抛物线交于点P(x1,y1)和Q(x2,y2),与直线AB交于点N(x3,y3),若x3<x1<x2,结合函数的图象,直接写出x1+x2+x3的取值范围为.
与抛物线交于点P(x1,y1)和Q(x2,y2),与直线AB交于点N(x3,y3),若x3<x1<x2,结合函数的图象,直接写出x1+x2+x3的取值范围为.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
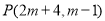 ,试分别根据下列条件,求出点
,试分别根据下列条件,求出点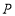 的坐标.
的坐标.(1)点
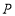 在
在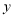 轴上;
轴上;(2)点
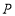 的纵坐标比横坐标大3;
的纵坐标比横坐标大3;(3)点
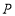 到
到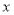 轴的距离为2,且在第四象限.
轴的距离为2,且在第四象限. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线AB∥CD.
(1)如图1,直接写出∠ABE,∠CDE和∠BED之间的数量关系是 .
(2)如图2,BF,DF分别平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.
(3)如图3,点E在直线BD的右侧,BF,DF仍平分∠ABE,∠CDE,请直接写出∠BFD和∠BED的数量关系 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,∠BAD=60°
(1) 如图1,点E为线段AB的中点,连接DE、CE.若AB=4,求线段EC的长
(2) 如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,线段MN与AD交于点G,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论
(3) 在(2)的条件下,若AC=
 ,请你直接写出DM+CN的最小值
,请你直接写出DM+CN的最小值
相关试题

