【题目】在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=90°﹣∠B,④∠A=∠B= ![]() ∠C中,能确定△ABC是直角三角形的条件有( )
∠C中,能确定△ABC是直角三角形的条件有( )
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】D
【解析】解:①∵∠A+∠B=∠C,∠A+∠B+∠C=180°, ∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,∴①正确;
②∵∠A:∠B:∠C=1:2:3,∠A+∠B+∠C=180°,
∴∠C= ![]() ×180°=90°,
×180°=90°,
∴△ABC是直角三角形,∴②正确;
③∵∠A=90°﹣∠B,
∴∠A+∠B=90°,
∵∠A+∠B+∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,∴③正确;
④∵∠A=∠B= ![]() ∠C,
∠C,
∴∠C=2∠A=2∠B,
∵∠A+∠B+∠C=180°,
∴∠A+∠A+2∠A=180°,
∴∠A=45°,
∴∠C=90°,
∴△ABC是直角三角形,∴④正确;
故选D.
根据三角形的内角和定理得出∠A+∠B+∠C=180°,再根据已知的条件逐个求出∠C的度数,即可得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,A(0,4),B(﹣3,0),C(2,0),D为B点关于AC的对称点,反比例函数y=
 的图象经过D点.
的图象经过D点.
(1)证明四边形ABCD为菱形;
(2)求此反比例函数的解析式;
(3)已知在y=
 的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.
的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BF平行于正方形ABCD的对角线AC,点E在BF上,且AE=AC,CF∥AE,则∠BCF的度数为 .
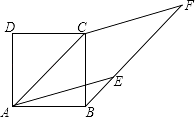
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
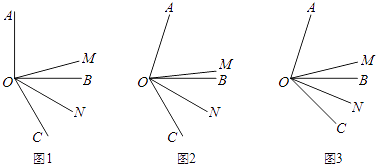
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知(x2+px+8)(x2-3x+q)的展开式中不含x2,x3项,求p、q的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:已知:(x﹣3)2
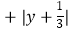 =0,求3x2y﹣[2xy2﹣2(xy﹣
=0,求3x2y﹣[2xy2﹣2(xy﹣ 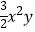 )+3xy]+5xy2的值.
)+3xy]+5xy2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个六棱柱的顶点个数、棱的条数、面的个数分别是( )
A. 6、12、6 B. 12、18、8
C. 18、12、6 D. 18、18、24
相关试题

