【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E. 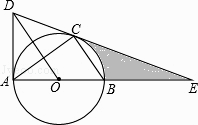
(1)求证:DE是⊙O的切线;
(2)若AE=6,CE=2 ![]() ,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
参考答案:
【答案】
(1)解:连结OC,如图,
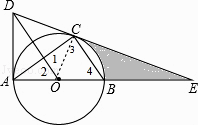
∵AD为⊙O的切线,
∴AD⊥AB,
∴∠BAD=90°,
∵OD∥BC,
∴∠1=∠3,∠2=∠4,
∵OB=OC,
∴∠3=∠4,
∴∠1=∠2,
在△OCD和△OAD中,
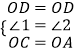 ,
,
∴△AOD≌△COD(SAS);
∴∠OCD=∠OAD=90°,
∴OC⊥DE,
∴DE是⊙O的切线;
(2)解:设半径为r,则OE=AE﹣OA=6﹣r,OC=r,
在Rt△OCE中,∵OC2+CE2=OE2,
∴r2+(2 ![]() )2=(6﹣r)2,解得r=2,
)2=(6﹣r)2,解得r=2,
∵tan∠COE= ![]() =
= ![]() =
= ![]() ,
,
∴∠COE=60°,
∴S阴影部分=S△COE﹣S扇形BOC
= ![]() ×2×2
×2×2 ![]() ﹣
﹣ ![]()
=2 ![]() ﹣
﹣ ![]() π.
π.
【解析】(1)连结OC,如图,先根据切线的性质得∠BAD=90°,再根据平行线的性质,由OD∥BC得∠1=∠3,∠2=∠4,加上∠3=∠4,则∠1=∠2,接着证明△AOD≌△COD,得到∠OCD=∠OAD=90°,于是可根据切线的判定定理得到DE是⊙O的切线;(2)设半径为r,则OE=AE﹣OA=6﹣r,OC=r,在Rt△OCE中利用勾股定理得到r2+(2 ![]() )2=(6﹣r)2 , 解得r=2,再利用正切函数求出∠COE=60°,然后根据扇形面积公式和S阴影部分=S△COE﹣S扇形BOC进行计算即可.
)2=(6﹣r)2 , 解得r=2,再利用正切函数求出∠COE=60°,然后根据扇形面积公式和S阴影部分=S△COE﹣S扇形BOC进行计算即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠BAC=90°,D是AC的中点,CE⊥BD于点E,交BA的延长线于点F.若BF=12,则△FBC的面积为( )

A. 40 B. 46 C. 48 D. 50
-
科目: 来源: 题型:
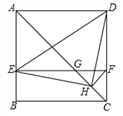
查看答案和解析>>【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作
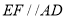 ,与AC、DC分别交于点
,与AC、DC分别交于点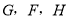 为CG的中点,连结DE、EH、DH、
为CG的中点,连结DE、EH、DH、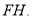 下列结论:
下列结论: 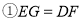 ;
; 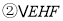 ≌
≌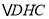 ;
; 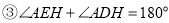 ;
; 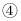 若
若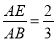 ,则
,则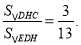 其中结论正确的有
其中结论正确的有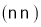
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
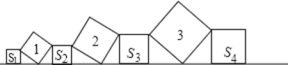
查看答案和解析>>【题目】在直线L上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放置的四个正方形的面积依次是
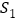 、
、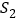 、
、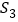 、
、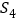 ,则
,则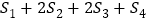 =( )
=( )
A. 5 B. 4 C. 6 D. 、10
-
科目: 来源: 题型:
查看答案和解析>>【题目】耐心算一算:
(1)﹣3﹣7;
(2)﹣(﹣7)﹣(﹣5)+(﹣4)
(3)
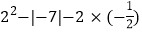
(4)(﹣81)÷
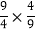 ÷(﹣16)
÷(﹣16)(5)
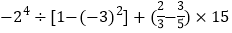
-
科目: 来源: 题型:
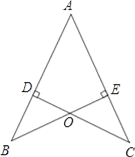
查看答案和解析>>【题目】如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证:AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正确的结论有________(填序号).

相关试题

