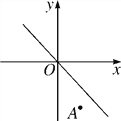
【题目】小明从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:①abc>0;②a﹣b+c<0;③b+2c>0; ④a﹣2b+4c>0;⑤2a=3b
你认为其中正确信息的个数有( )
A.2个
B.3个
C.4个
D.5个
参考答案:
【答案】C
【解析】解:
∵抛物线开口向下,与y轴的交点位于x轴的上方,
∴a<0,c>0,
∵对称轴为x=﹣ ![]() =﹣
=﹣ ![]() ,
,
∴2a=3b<0,
∴abc>0,故①⑤正确;
∵当x=﹣1时,y>0,当x=﹣ ![]() 时,y>0
时,y>0
∴a﹣b+c>0,故②不正确;
∴ ![]() a﹣
a﹣ ![]() b+c>0,即a﹣2b+4c>0,故④正确;
b+c>0,即a﹣2b+4c>0,故④正确;
∵a﹣b+c>0,2a=3b,
∴ ![]() b﹣b+c>0,即b+2c>0,故③正确;
b﹣b+c>0,即b+2c>0,故③正确;
综上可知正确的有①③④⑤共4个,
故选C.
【考点精析】解答此题的关键在于理解二次函数图象以及系数a、b、c的关系的相关知识,掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).
-
科目: 来源: 题型:
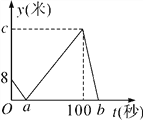
查看答案和解析>>【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒,在跑步过程中,甲、乙两人间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②c=92;③b=123.其中正确的是( )
A. ①②
B. ②③
C. ①③
D. ①②③
-
科目: 来源: 题型:
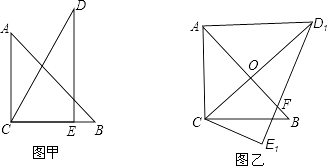
查看答案和解析>>【题目】把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=12,DC=14,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与 CD1交于点O,则线段AD1的长为( )
A.6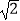
B.10
C.8
D.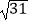
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将直线y=-x沿y轴向下平移后的直线恰好经过点A(2,-4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】永州市是一个降水丰富的地区,今年4月初,某地连续降雨导致该地某水库水位持续上涨,下表是该水库4月1日~4月4日的水位变化情况:
日期x
1
2
3
4
水位y(米)
20.00
20.50
21.00
21.50
(1)请建立该水库水位y与日期x之间的函数模型;
(2)请用求出的函数表达式预测该水库今年4月6日的水位;
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(0,5),直线x=-5与x轴交于点D,直线y=-
 x-
x- 与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.
与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.(1)求点C,E的坐标及直线AB的解析式;
(2)若S=S△CDE+S四边形ABDO,求S的值;
(3)在求(2)中S时,嘉琪有个想法:“将△CDE沿x轴翻折到△CDB的位置,而△CDB与四边形ABDO拼接后可看成△AOC,这样求S便转化为直接求△AOC的面积,如此不更快捷吗?”但大家经反复验算,发现S△AOC≠S,请通过计算解释他的想法错在哪里.

-
科目: 来源: 题型:
查看答案和解析>>【题目】根据题意设未知数,并列出方程(不必求解).
(1)有两个工程队,甲队人数30名,乙队人数10名,问怎样调整两队的人数,才能使甲队的人数是乙队人数的7倍.
(2)有一个班的同学准备去划船,租了若干条船,他们计算了一下,如果比原计划多租1条船,那么正好每条船坐6人;如果比原计划少租1条船,那么正好每条船坐9人.问这个班共有多少名同学?
相关试题

