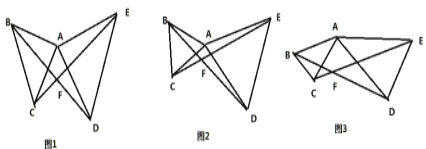
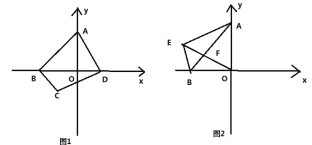
【题目】(1)如图 1,△ABC 和△ADE 都是等腰直角三角形,∠BAC 和∠DAE 是直角,连接BD,CE 相交于点 F,则∠BFC= °
(2)如图 2,△ABC 和△ADE 都是等边三角形,连接 BD,CE 相交于点 F,则∠BFC= °
(3)如图 3,△ABC 和△ADE 都是等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE,连接 BD,CE相交于点 F,请猜想∠BFC 与∠BAC 有怎样的大小关系?请证明你的猜想
参考答案:
【答案】(1)90°;(2)60°;(3)![]() 证明见解析;
证明见解析;
【解析】
(1)求出![]() 根据SAS证出
根据SAS证出![]() ≌
≌![]() 即可.
即可.
(2)求出![]() 根据SAS证出
根据SAS证出![]() ≌
≌![]() 即可.
即可.
(3)根据![]() 根据SAS证出
根据SAS证出![]() ≌
≌![]() 即可.
即可.
(1)如图:
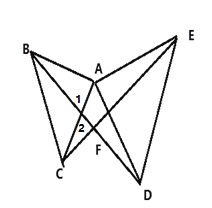
∵△ABC和△ADE都是等腰直角三角形
∴AD=AE,AB=AC,![]()
又∵![]()
∴∠DAB=∠EAC,
∵在△ADB和△AEC中
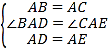 ,
,
∴△ADB≌△AEC(SAS),
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
故答案为:90°
(2)如图:
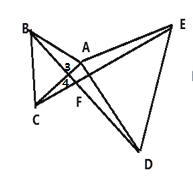
∵△ABC和△ADE都是等边三角形
∴AD=AE,AB=AC,![]()
又∵![]()
∴∠DAB=∠EAC,
∵在△ADB和△AEC中
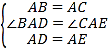 ,
,
∴△ADB≌△AEC(SAS),
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
故答案为:60°
(3) ![]() 理由如下:
理由如下:
∵∠BAC=∠DAE
又∵![]()
∴∠DAB=∠EAC,
∵在△ADB和△AEC中
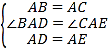 ,
,
∴△ADB≌△AEC(SAS),
∴![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 中,点 D,E 分别在∠ABC 和∠ACB 的平分线上,连接 BD,DE,EC,若∠D+∠E=295°, 则∠A 是( )
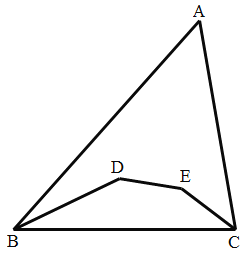
A.65°B.60°C.55°D.50°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 和直线
和直线 .我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.
.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.下列判断: ①当x>2时,M=y2;
②当x<0时,x值越大,M值越大;
③使得M大于4的x值不存在;
④若M=2,则x= 1 .
其中正确的有

A.1个 B.2个 C. 3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点 A,B,C 的坐标分别是(2,1),(6,1),(3,5),若△A1B1C1 与△ABC 关于x 轴对称
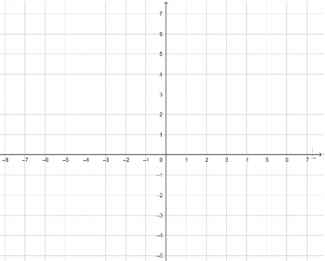
(1)在平面直角坐标系中画出△A1B1C1,并写出 A1,B1,C1 三个点的坐标
(2)求出△A1B1C1的面积
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 1,在平面直角坐标系中,A,B,D 三点的坐标是(0,2),(-2,0),(1,0),点C 是 x 轴下方一点,且 CD⊥AD,∠BAD+∠BCD=180°,AD=CD
(1)求证:BD 平分∠ABC
(2)求四边形 ABCD 的面积
(3)如图 2,BE 是∠ABO 的邻补角的平分线,连接 AE,OE 交 AB 于点 F,若∠AEO=45°,求证:AF=AO.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某弹簧挂上不超过20千克的物体后按一定规律伸长,测得一弹簧的长度
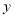 (厘米)与所挂的物体的质量
(厘米)与所挂的物体的质量 (千克)有下面的关系:
(千克)有下面的关系:
0
1
2
3
4
5
6
7
8
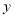
12
12.5
13
13.5
14
14.5
15
15.5
16
那么弹簧的总长
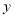 (厘米)与所挂的物体的质量
(厘米)与所挂的物体的质量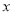 (千克)之间是否是函数关系?若是,请写出函数关系式.
(千克)之间是否是函数关系?若是,请写出函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点(﹣2,y1),(﹣5
 ,y2),(1
,y2),(1 ,y3)在函数y=2x2+8x+7的图象上,则y1,y2,y3的大小关系为_____.
,y3)在函数y=2x2+8x+7的图象上,则y1,y2,y3的大小关系为_____.
相关试题

