【题目】如图乙,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1)如图甲,将△ADE绕点A 旋转,当C、D、E在同一条直线上时,连接BD、BE,则下列给出的四个结论中,其中正确的是 .
①![]() ②
②![]() ③
③![]() ④
④![]()
(2)若AB=4,AD=2,把△ADE绕点A旋转,
①当∠EAC=90°时,求PB的长;
②求旋转过程中线段PB长的最大值.

参考答案:
【答案】(1)①②③;
(2)PB的长为![]() 或
或![]() ;
;
(3)PB长的最大值是![]() .
.
【解析】分析:(1)①由条件证明△ABD≌△ACE,就可以得到结论;②由△ABD≌△ACE就可以得出∠ABD=∠ACE,就可以得出∠BDC=90°而得出结论;③由条件知∠ABC=∠ABD+∠DBC=45°,由∠DBC+∠ACE=90°,就可以得出结论;④△BDE为直角三角形就可以得出BE=BD+DE,由△DAE和△BAC是等腰直角三角形就有DE=2AD,BC=2AB,就有BC=BD+CD2≠BD就可以得出结论.(2)①分两种情形a、如图2中,当点E在AB上时,BE=AB-AE=1.由△PEB∽△AEC,得![]() ,由此即可解决问题.b、如图3中,当点E在BA延长线上时,BE=3.解法类似.②如图5中,以A为圆心AD为半径画圆,当CE在 A上方与 A相切时,PB的值最大.求出PB即可.
,由此即可解决问题.b、如图3中,当点E在BA延长线上时,BE=3.解法类似.②如图5中,以A为圆心AD为半径画圆,当CE在 A上方与 A相切时,PB的值最大.求出PB即可.
本题解析:(1)①②③
(2)①解:a、如图2中,当点E在AB上时,BE=AB﹣AE=2.
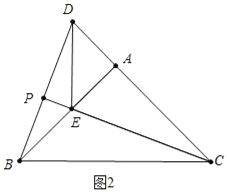
∵∠EAC=90°,∴CE=![]() ,
,
同(1)可证△ADB≌△AEC.
∴∠DBA=∠ECA.∵∠PEB=∠AEC,∴△PEB∽△AEC.
∴![]() ,∴
,∴![]() ,∴PB=
,∴PB=![]() ,
,
b、如图3中,当点E在BA延长线上时,BE=6.
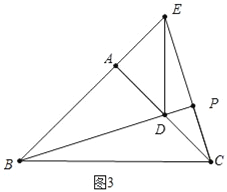
∵∠EAC=90°,∴CE=![]() ,
,
同(1)可证△ADB≌△AEC.
∴∠DBA=∠ECA.∵∠BEP=∠CEA,∴△PEB∽△AEC,
∴![]() ,∴
,∴![]() ,∴PB=
,∴PB=![]() ,
,
综上,PB=![]() 或
或![]() .
.
②解:如图5中,以A为圆心AD为半径画圆,当CE在⊙A上方与⊙A相切时,PB的值最大.
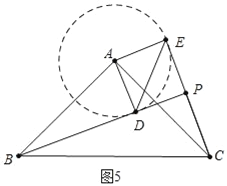
理由:此时∠BCE最大,因此PB最大,(△PBC是直角三角形,斜边BC为定值,∠BCE最大,因此PB最大)
∵AE⊥EC,∴EC=![]() ,
,
由(1)可知,△ABD≌△ACE,
∴∠ADB=∠AEC=90°,BD=CE=2![]() ,∴∠ADP=∠DAE=∠AEP=90°,
,∴∠ADP=∠DAE=∠AEP=90°,
∴四边形AEPD是矩形,∴PD=AE=2,∴PB=BD+PD=2![]() +2.
+2.
综上所述,PB长的最大值是2![]() +2.
+2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程kx2+2x﹣1=0有两个不相等的实数根,则k的取值范围是( )
A.k>﹣1
B.k>1
C.k≠0
D.k>﹣1且k≠0 -
科目: 来源: 题型:
查看答案和解析>>【题目】在三角形ABC中,AB=AC,BC=5 cm,作AB的垂直平分线交AC于点D,连接BD,如果△BCD的周长是17 cm,那么AB的长为( )
A. 12 cm B. 6 cm C. 7 cm D. 5 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
一艘船从甲码头到乙码头顺流而行,用了2.5h;从乙码头返回甲码头逆流而行,用了3h.已知水流的速度是3.5km/h,求船在静水中的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的三边是三个连续的奇数,最长边是2k+5(k为大于1的整数),则其它两边分别分别是 和 ,猜想:这个三角形的最长边与最短边之和与第三边有何关系,试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正多边形的内角和等于720°,那么这个正多边形的每一个外角等于( )
A.45°B.60°C.120°D.135°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AB上一点,D为线段AC的中点,E为线段CB的中点.
(1)如果AB=6 cm,BC=4 cm,试求线段DE的长;
(2)如果AB=a cm,试求线段DE的长;
(3)若C在线段AB的延长线上,且满足AC-BC=b cm,D,E分别为AC,BC的中点,你能猜想出线段DE的长度吗?写出你的结论,不用说明理由.
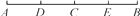
相关试题

