【题目】列方程解应用题:
一艘船从甲码头到乙码头顺流而行,用了2.5h;从乙码头返回甲码头逆流而行,用了3h.已知水流的速度是3.5km/h,求船在静水中的平均速度.
参考答案:
【答案】38.5km/h.
【解析】
等量关系为:顺水速度×顺水时间=逆水速度×逆水时间.即:2.5×(静水速度+水流速度)=3×(静水速度﹣水流速度).
解:设船在静水中的平均速度为xkm/h,依题意得:
2.5(x+3.5)=3(x﹣3.5),
解得:x=38.5,
答:船在静水中的平均速度为38.5km/h.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上A,B两点对应的有理数分别为10和15,点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.

(1)当0<t<5时,用含t的式子填空:
BP=_______,AQ=_______;
(2)当t=2时,求PQ的值;
(3)当PQ=
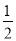 AB时,求t的值.
AB时,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程kx2+2x﹣1=0有两个不相等的实数根,则k的取值范围是( )
A.k>﹣1
B.k>1
C.k≠0
D.k>﹣1且k≠0 -
科目: 来源: 题型:
查看答案和解析>>【题目】在三角形ABC中,AB=AC,BC=5 cm,作AB的垂直平分线交AC于点D,连接BD,如果△BCD的周长是17 cm,那么AB的长为( )
A. 12 cm B. 6 cm C. 7 cm D. 5 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图乙,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1)如图甲,将△ADE绕点A 旋转,当C、D、E在同一条直线上时,连接BD、BE,则下列给出的四个结论中,其中正确的是 .
①
 ②
② ③
③ ④
④
(2)若AB=4,AD=2,把△ADE绕点A旋转,
①当∠EAC=90°时,求PB的长;
②求旋转过程中线段PB长的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的三边是三个连续的奇数,最长边是2k+5(k为大于1的整数),则其它两边分别分别是 和 ,猜想:这个三角形的最长边与最短边之和与第三边有何关系,试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正多边形的内角和等于720°,那么这个正多边形的每一个外角等于( )
A.45°B.60°C.120°D.135°
相关试题

