【题目】在直角坐标系种中,点![]()
![]() 点
点![]() 关于
关于![]() 轴对称的点的坐标是:________;
轴对称的点的坐标是:________;
![]() 点
点![]() 关于
关于![]() 轴对称的点的坐标是:________;
轴对称的点的坐标是:________;
![]() 点
点![]() 关于原点对称的点的坐标是:________;
关于原点对称的点的坐标是:________;
![]() 将点
将点![]() 绕原点逆时针旋转
绕原点逆时针旋转![]() 后,得到的点的坐标是:________;
后,得到的点的坐标是:________;
![]() 将点
将点![]() 绕原点顺时针旋转
绕原点顺时针旋转![]() 后,得到的点的坐标是:________;
后,得到的点的坐标是:________;
![]() 将点
将点![]() 绕另一点
绕另一点![]() 旋转
旋转![]() 得到点
得到点![]() ,则
,则![]() 点的坐标为________.
点的坐标为________.
参考答案:
【答案】![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
【解析】
(1)、(2)根据关于x轴和y轴对称的点的坐标特征求解;
(3)利用关于原点对称的点的坐标特征求解;
(4)将点P绕原点逆时针旋转90°后得到的点与点P关于y轴对称,与(2)一样求解;
(5)将点P绕原点顺时针旋转135°后得到的点与点P关于x轴对称,与(1)一样求解;
(6)PQ的垂直平分线为x轴,则M点在x轴上,当点P绕另一点M顺时针旋转45°得到点Q,则OM=OP,于是得到此时M(- ![]() ,0);当点P绕另一点M逆时针旋转45°得到点Q时,写出点(-
,0);当点P绕另一点M逆时针旋转45°得到点Q时,写出点(- ![]() ,0)关于直线PQ的对称点即可.
,0)关于直线PQ的对称点即可.
(1)点P关于x轴对称的点的坐标是:(1,-1);
(2)点P关于y轴对称的点的坐标是:(-1,1);
(3)点P关于原点对称的点的坐标是:(-1,-1);
(4)将点P绕原点逆时针旋转90°后,得到的点的坐标是:(-1,1);
(5)将点P绕原点顺时针旋转135°后,得到的点的坐标是:(0,-![]() );
);
(6)将点P绕另一点M旋转45°得到点Q(1,-1),则M点的坐标为(-![]() ,0),(2+
,0),(2+![]() ,0).
,0).
故答案是:(1). ![]() (2).
(2). ![]() (3).
(3). ![]() (4).
(4). ![]() (5).
(5). ![]() (6).
(6). ![]() ,
,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学研究课上,老师出示如图1所示的长方形纸条
 ,
, ,
, ,然后在纸条上任意画一条截线段
,然后在纸条上任意画一条截线段 ,将纸片沿
,将纸片沿 折叠,
折叠,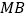 与
与 交于点
交于点 ,得到
,得到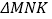 ,如图2所示:
,如图2所示:
(1)若
 ,求
,求 的大小;
的大小;(2)改变折痕
 位置,判断
位置,判断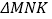 的形状,并说明理由;
的形状,并说明理由;(3)爱动脑筋的小明在研究
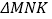 的面积时,发现
的面积时,发现 边上的高始终是个不变的值.根据这一发现,他很快研究出
边上的高始终是个不变的值.根据这一发现,他很快研究出 的面积最小值为
的面积最小值为 ,求
,求 的大小;
的大小;(4)小明继续动手操作,发现了
 面积的最大值,请你求出这个最大值.
面积的最大值,请你求出这个最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )
A.k>
B.k≥
C.k> 且k≠1
且k≠1
D.k≥ 且k≠1
且k≠1 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是轴对称图形,又是中心对称的是( )
A.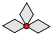
B.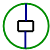
C.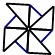
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=kx2﹣7x﹣7的图象与x轴没有交点,则k的取值范围为( )
A.k>﹣
B.k≥﹣ 且k≠0
且k≠0
C.k<﹣
D.k>﹣ 且k≠0
且k≠0 -
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若A的对应点A2的坐标为(0,4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 在平面直角坐标系中,将点
在平面直角坐标系中,将点 向右平移
向右平移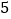 个单位到点
个单位到点 ,再将点
,再将点 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转 到点
到点 .直接写出点
.直接写出点 ,
, 的坐标;23.
的坐标;23. 在平面直角坐标系中,将第二象限内的点
在平面直角坐标系中,将第二象限内的点 向右平移
向右平移 个单位到第一象限点
个单位到第一象限点 ,再将点
,再将点 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转 到点
到点 ,直接写出点
,直接写出点 ,
, 的坐标;
的坐标; 在平面直角坐标系中.将点
在平面直角坐标系中.将点 沿水平方向平移
沿水平方向平移 个单位到点
个单位到点 ,再将点
,再将点 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转 到点
到点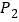 ,直接写出点
,直接写出点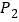 的坐标.
的坐标.
相关试题

