【题目】![]() 在平面直角坐标系中,将点
在平面直角坐标系中,将点![]() 向右平移
向右平移![]() 个单位到点
个单位到点![]() ,再将点
,再将点![]() 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转![]() 到点
到点![]() .直接写出点
.直接写出点![]() ,
,![]() 的坐标;23.
的坐标;23.
![]() 在平面直角坐标系中,将第二象限内的点
在平面直角坐标系中,将第二象限内的点![]() 向右平移
向右平移![]() 个单位到第一象限点
个单位到第一象限点![]() ,再将点
,再将点![]() 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转![]() 到点
到点![]() ,直接写出点
,直接写出点![]() ,
,![]() 的坐标;
的坐标;
![]() 在平面直角坐标系中.将点
在平面直角坐标系中.将点![]() 沿水平方向平移
沿水平方向平移![]() 个单位到点
个单位到点![]() ,再将点
,再将点![]() 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转![]() 到点
到点![]() ,直接写出点
,直接写出点![]() 的坐标.
的坐标.
参考答案:
【答案】见解析
【解析】
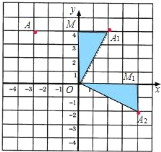
(1)如图,由于将点A(-3,4)向右平移5个单位到点A1,根据平移规律可以得到A1的坐标,又将点A1绕坐标原点顺时针旋转90°到点A2,根据旋转得到△OMA1≌△OM1A2,由此就可以确定A2的坐标;
(2)可以利用(1)中的规律依次分别得到B1的坐标,B2的坐标;
(3)分两种情况:①当把点P(c,d)沿水平方向右平移n个单位到点P1,此时可以利用(2)的规律求出P1和P2的坐标;②当把点P(c,d)沿水平方向左平移n个单位到点P1,那么P1的横坐标和前面的计算方法恰好相反,用减法,然后将点P1绕坐标原点顺时针旋转90°到点P2的坐标的规律也恰好相反,由此可以直接得到P2的坐标.
![]() 如图,∵将点
如图,∵将点![]() 向右平移
向右平移![]() 个单位到点
个单位到点![]() ,
,
∴![]() 的坐标为
的坐标为![]() ,
,
∵又将点![]() 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转![]() 到点
到点![]() ,
,
∴![]() ,
,
∴![]() 的坐标
的坐标![]() .
.
![]() 根据
根据![]() 中的规律得:
中的规律得:
![]() 的坐标为
的坐标为![]() ,
,![]() 的坐标为
的坐标为![]() .
.![]() 分两种情况:
分两种情况:
①当把点![]() 沿水平方向右平移
沿水平方向右平移![]() 个单位到点
个单位到点![]() ,
,
∴![]() 的坐标为
的坐标为![]() ,
,
则![]() 的坐标为
的坐标为![]() ;
;
②当把点![]() 沿水平方向左平移
沿水平方向左平移![]() 个单位到点
个单位到点![]() ,
,
∴![]() 的坐标为
的坐标为![]() ,
,
然后将点![]() 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转![]() 到点
到点![]() ,
,
∴![]() 的坐标
的坐标![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系种中,点
 点
点 关于
关于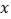 轴对称的点的坐标是:________;
轴对称的点的坐标是:________; 点
点 关于
关于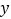 轴对称的点的坐标是:________;
轴对称的点的坐标是:________; 点
点 关于原点对称的点的坐标是:________;
关于原点对称的点的坐标是:________; 将点
将点 绕原点逆时针旋转
绕原点逆时针旋转 后,得到的点的坐标是:________;
后,得到的点的坐标是:________; 将点
将点 绕原点顺时针旋转
绕原点顺时针旋转 后,得到的点的坐标是:________;
后,得到的点的坐标是:________; 将点
将点 绕另一点
绕另一点 旋转
旋转 得到点
得到点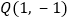 ,则
,则 点的坐标为________.
点的坐标为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=kx2﹣7x﹣7的图象与x轴没有交点,则k的取值范围为( )
A.k>﹣
B.k≥﹣ 且k≠0
且k≠0
C.k<﹣
D.k>﹣ 且k≠0
且k≠0 -
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若A的对应点A2的坐标为(0,4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
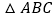 的顶点坐标分别为
的顶点坐标分别为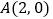 ,
,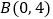 ,
,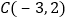 .
.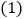 如图
如图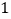 ,求
,求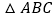 的面积.
的面积.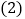 若点
若点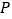 的坐标为
的坐标为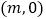 ,
,①请直接写出线段
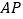 的长为________(用含
的长为________(用含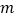 的式子表示);
的式子表示);②当
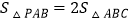 时,求
时,求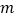 的值.
的值.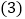 如图
如图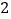 ,若
,若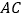 交
交 轴于点
轴于点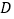 ,直接写出点
,直接写出点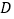 的坐标为________.
的坐标为________.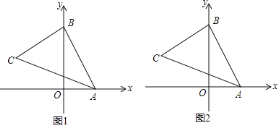
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把抛物线y=
 x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=  x2交于点Q,则图中阴影部分的面积为 .
x2交于点Q,则图中阴影部分的面积为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=
 BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE= BC,成立的个数有( )
BC,成立的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

