【题目】在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)如图1,求证:四边形![]() 是菱形;
是菱形;

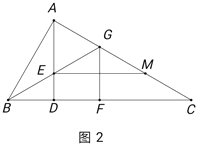
(2)如图2,若![]() 为
为![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,在不添加任何辅助线的情况下,请直接写出图2中是
,在不添加任何辅助线的情况下,请直接写出图2中是![]() 长
长![]() 倍的所有线段.
倍的所有线段.
参考答案:
【答案】(1)证明见解析;(2)AB、BF、CF、EM.
【解析】
(1)先证明四边形AEFG是平行四边形,再证明AE=AG即可;
(2)先证明AB=![]() AG,再分别证明AB=BF=CF=EM,CM=AG即可.
AG,再分别证明AB=BF=CF=EM,CM=AG即可.
解:(1)∵AD⊥BC,GF⊥BC,

∴∠ADF=∠GFC=90°,
∴AE∥GF,
在△ABG和△FBG中, ,
,
∴△ABG≌△FBG,
∴AG=FG,
∵∠FBG+∠BED=90°,
∵∠BED=∠AEG,
∴∠FBG+∠AEG=90°,
∵∠ABG+∠AGE=90°,
∵∠ABG=∠FBG,
∴∠AEG=∠AGE,
∴AE=AG,
∴AE=FG,
∴四边形AEFG是平行四边形,
∵AE=AG∴四边形AEFG是菱形.
(2)∵四边形AEFG是菱形,
∴AE=AG,
∵BE=EG,∠BAG=90°,
∴AE=BE=EG,
∴△AEG是等边三角形,
∴∠AGE=60°,
在RT△ABG中,∵∠ABG=30°,
∴AB=![]() AG,
AG,
∵∠C=30°,∴BC=2AB,
∴BE=GE,EF∥AC,EM∥BC,
∴BF=FC,CM=GM,
在RT△AEM中,∵∠AME=∠C=30°,∠GEM+∠GME=60°,
∴∠GEM=∠GME=30°,
∴EG=AG=GM=CM,
∵EM∥FC,EF∥CM,
∴四边形EFCM是平行四边形,
∴AB=BF=CF=EM=![]() CM,
CM,
∴是CM长![]() 倍的所有线段有AB、BF、CF、EM.
倍的所有线段有AB、BF、CF、EM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二孩子政策的落实引起了全社会的关注,某校学生数学兴趣小组为了了解本校同学父母生育二孩子的态度,在学校抽取了部分同学对父母生育二孩子所持的态度进行了问卷调查,调查分别为非常赞同、赞同、无所谓、不赞同等四种态度,现将调查统计结果制成了如图两幅统计图,请结合两幅统计图,回答下列问题:
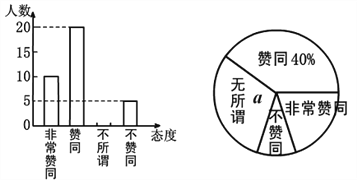
(1)在这次问卷调查中一共抽取了__________名学生,a=________%;
(2)请补全条形统计图;
(3)持“不赞同”态度的学生人数的百分比所占扇形的圆心角为__________度;
(4)若该校有3000名学生,请你估计该校学生对父母生育二孩子持“赞同”和“非常赞同”两种态度的人数之和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①、图②是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段
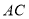 的两个端点均在小正方形的顶点上.
的两个端点均在小正方形的顶点上.
(1)如图①,点
 在小正方形格点上,在图①中作出点
在小正方形格点上,在图①中作出点 关于直线
关于直线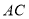 的对称点
的对称点 ,连接
,连接 、
、 、
、 、
、 ,并直接写出四边形
,并直接写出四边形 的周长;
的周长;(2)在图②中画出一个以线段
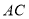 为一条对角线、面积为15的菱形
为一条对角线、面积为15的菱形 ,且点
,且点 和点
和点 均在小正方形的顶点上.
均在小正方形的顶点上. -
科目: 来源: 题型:
查看答案和解析>>【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
-
科目: 来源: 题型:
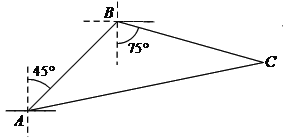
查看答案和解析>>【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,菱形
 中,
中,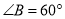 ,
,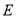 、
、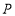 分别是边
分别是边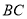 和
和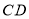 上的点,且
上的点,且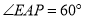 .
.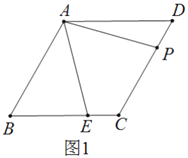
(1)求证:
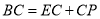
(2)如图2,
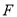 在
在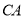 延长线上,且
延长线上,且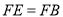 ,求证:
,求证: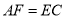
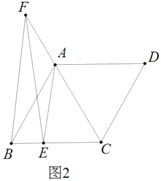
(3)如图3,在(2)的条件下,
 ,
, ,
, 是
是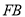 的中点,求
的中点,求 的长.
的长.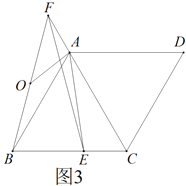
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情景:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
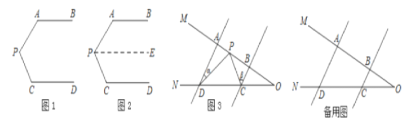
(1)天天同学看过图形后立即口答出:∠APC=110°,请你补全他的推理依据.
如图2,过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD.(___)
∴∠A+∠APE=180°.
∠C+∠CPE=180°.(___)
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°
∴∠APC=∠APE+∠CPE=110°.(___)
问题迁移:
(2)如图3,AD∥BC,当点P在A. B两点之间运动时,∠ADP=∠α,∠BCP=∠β,求∠CPD与∠α、∠β之间有何数量关系?请说明理由。
(3)在(2)的条件下,如果点P在A. B两点外侧运动时(点P与点A. B. O三点不重合),请你直接写出∠CPD与∠α、∠β之间的数量关系.
相关试题

