【题目】(1)如图①,在等边△ABC中,点M是BC边上的任意一点(不含端点B,C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ACN=∠ABC.
【类比探究】
(2)如图②,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ACN=∠ABC还成立吗?请说明理由.
【拓展延伸】
(3)如图③,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.

参考答案:
【答案】(1)答案见解析;(2)∠ACN=∠ABC还成立;(3)∠ABC=∠ACN.
【解析】试题分析:(1)利用SAS可证明△BAM≌△CAN,继而得出结论;
(2)也可以通过证明△BAM≌△CAN,得出结论,和(1)的思路完全一样.
(3)首先得出∠BAC=∠MAN,从而判定△ABC∽△AMN,得到![]() ,根据∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,得到∠BAM=∠CAN,从而判定△BAM∽△CAN,即可得出结论.
,根据∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,得到∠BAM=∠CAN,从而判定△BAM∽△CAN,即可得出结论.
试题解析:解:(1)∵△ABC、△AMN是等边三角形,∴AB=AC,AM=AN,∠BAC=∠MAN=60°,∴∠BAM=∠CAN,在△BAM和△CAN中,∵AB=AC,∠BAM=∠CAN,AM=AN,∴△BAM≌△CAN(SAS),∴∠ABC=∠ACN.
(2)结论∠ABC=∠ACN仍成立;
理由如下:∵△ABC、△AMN是等边三角形,∴AB=AC,AM=AN,∠BAC=∠MAN=60°,∴∠BAM=∠CAN,在△BAM和△CAN中,∵AB=AC,∠BAM=∠CAN,AM=AN,∴△BAM≌△CAN(SAS),∴∠ABC=∠ACN.
(3)∠ABC=∠ACN;
理由如下:∵BA=BC,MA=MN,顶角∠ABC=∠AMN,∴底角∠BAC=∠MAN,∴△ABC∽△AMN,∴ ![]() ,又∵∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,∴∠BAM=∠CAN,∴△BAM∽△CAN,∴∠ABC=∠ACN.
,又∵∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,∴∠BAM=∠CAN,∴△BAM∽△CAN,∴∠ABC=∠ACN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由两个长为8,宽为4的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是( )

A.15B.16C.19D.20
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点
 是线段
是线段 的中点,过点
的中点,过点 作
作 的垂线
的垂线 ,在射线
,在射线 上有一个动点
上有一个动点 (点
(点 不与端点
不与端点 重合),连接
重合),连接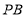 ,过点
,过点 作
作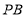 的垂线,垂足为点
的垂线,垂足为点 ,在射线
,在射线 上取点
上取点 ,使得
,使得 ,已知
,已知
(1)当
 时,求
时,求 的度数;
的度数;(2)过点
 作
作 垂直于直线
垂直于直线 交
交 于点
于点 ,在点
,在点 的运动过程中,
的运动过程中, 的大小随点
的大小随点 的运动而变化,在这个变化过程中线段
的运动而变化,在这个变化过程中线段 的长度是否发生变化?若不变,求出
的长度是否发生变化?若不变,求出 的长;若变化,请说明理由;
的长;若变化,请说明理由;(3)如图2,当
 时,设直线
时,设直线 与直线
与直线 相交于点
相交于点 ,求
,求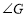 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】作图题
(1)如图①,点C是∠AOB边OB上的一点,在图中作出点C到OA的垂线段CD,垂足为D.再过C点作OA的平行线CE.
(2)如图②,在正方形网格中,每个小正方形的边长为1,△ABC的顶点都在正方形顶点上,将△ABC先向左平移2个单位,再向下平移3个单位,得到△A′B′C′,请你画出平移后的△A′B′C′.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,□ OABC的边OC落在x轴的正半轴上,点C(4,0),B(6,2),直线y=2x+1以每秒2个单位的速度向下平移,经过________秒该直线可将□OABC的面积平分.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M、N分别是正方形ABCD的边CD、CB上的动点,满足DM=CN,AM与DN相交于点E,连接CE,若正方形的边长为2,则线段CE的最小值是______________.

相关试题

