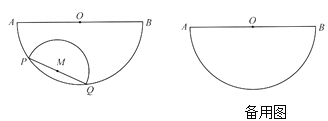
【题目】如图,半圆O的直径AB=4,以长为2的弦PQ为直径,向点O方向作半圆M,其中P点在AQ(弧)上且不与A点重合,但Q点可与B点重合.
发现 AP(弧)的长与QB(弧)的长之和为定值l,求l;
思考 点M与AB的最大距离为_______,此时点P,A间的距离为_______;点M与AB的最小距离为________,此时半圆M的弧与AB所围成的封闭图形面积为________.
探究 当半圆M与AB相切时,求AP(弧)的长.
(注:结果保留π,cos 35°=![]() ,cos 55°=
,cos 55°=![]() )
)
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ,2,
,2,![]() ,
,![]() ;(3)弧AP的长为
;(3)弧AP的长为![]() .
.
【解析】
试题分析:发现:连结OP,OQ,可得OP=OQ=PQ=2,即可得OP=OQ=PQ=2,根据弧长公式求得弧BC的长度,用半圆的弧长减去弧BC的长即可求得l的长;思考:当OM⊥AB时, 点M与AB的最大距离就是OM,△AOP是等边三角形,利用垂径定理和勾股定理即可得OM和PA的长,当Q与B重合点,点M与AB的距离最小,利用三角形的三边关系即可求得答案;探究:半圆M与AB相切,分两种情况①半圆M与AO切于点T时和②半圆M与BO切于点S时,分别求得弧AP的长即可.
试题解析:发现:连结OP,OQ,则OP=OQ=PQ=2.
∴∠POQ=60°,∴弧BC的长=![]() .
.
∴![]() .
.
思考:![]() ,2,
,2,![]() ,
,![]() .
.
探究:半圆M与AB相切,分两种情况:
①如图1,半圆M与AO切于点T时,连结PO,MO,TM.
则MT⊥AO,OM⊥PQ,
在Rt△POM中,sin∠POM=![]() ,
,
∴∠POM=30°,
在Rt△TOM中,TO=![]() ,
,
∴cos∠AOM=![]() ,即∠AOM=35°,
,即∠AOM=35°,
∴∠POA=35°-30°=5°.
∴弧AP的长=![]() .
.
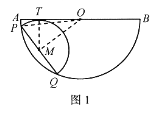
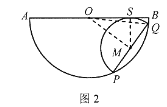
②如图2,半圆M与BO切于点S时,连结PO,MO,SM..
根据圆的对称性,同理得弧BQ的长为![]() ,
,
由![]() 得弧AP的长为
得弧AP的长为![]() .
.
综上,弧AP的长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数y=(m﹣1)x+m2﹣1的图象通过原点,则m的值为( )
A.m=﹣1
B.m=1
C.m=±1
D.m≠1 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是( )
A.两直线与第三条直线相交,同位角相等;
B.两直线与第三条直线相交,内错角相等
C.两直线平行,内错角相等;
D.两直线平行,同旁内角相等 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,相等的一组是( )
A. 23和32 B. |﹣2|3和|2|3
C. ﹣(+2)和|﹣2| D. (﹣2)2和﹣22
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级(1)班所有学生参加2016年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为A、B、C、D四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
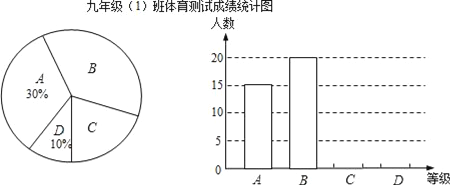
(1)九年级(1)班参加体育测试的学生有____人;
(2)将条形统计图补充完整;
(3)在扇形统计图中,等级B部分所占的百分比是____,等级C对应的圆心角的度数为____;
(4)若该校九年级学生共有850人参加体育测试,估计达到A级和B级的学生共有
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=3x+2沿y轴向下平移6个单位,则平移后直线解析式为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
(1)第1个等式:a1=
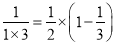 ; 第2个等式:a2=
; 第2个等式:a2= ;
;第3个等式:a3=
 ; 第4个等式:a4=
; 第4个等式:a4= ;
;…
用含有n的代数式表示第n个等式:an=___________=___________(n为正整数);
(2)按一定规律排列的一列数依次为
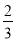 ,1,
,1, 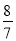 ,
, 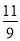 ,
, 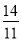 ,
, 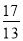 ,…,按此规律,这列数中的第100个数是_______________.
,…,按此规律,这列数中的第100个数是_______________.
相关试题

