【题目】在平面直角坐标系中,点A(0,a)、B(b,0)且a>|b|.
(1)若a、b满足a2+b2﹣4a﹣2b+5=0.
①求a、b的值;
②如图1,在①的条件下,将点B在x轴上平移,且b满足:0<b<2;在第一象限内以AB为斜边作等腰Rt△ABC,请用b表示S四边形AOBC , 并写出解答过程.
(2)若将线段AB沿x轴向正方向移动a个单位得到线段DE(D对应A,E对应B)连接DO,作EF⊥DO于F,连接AF、BF.
①如图2,判断AF与BF的关系并说明理由;
②若BF=OA﹣OB,求∠OAF的度数(直接写出结果).
参考答案:
【答案】解:(1)①∵a2+b2﹣4a﹣2b+5=0,
∴(a﹣2)2+(b﹣1)2=0,
∴a=2,b=1,
②∵A(0,2),B(b,0),
∴AB=![]() ,
,
∵△ABC是等腰直角三角形,
∴BC=![]() AB=
AB=![]() ,
,
∴S四边形AOBC=S△AOB+S△ABC=![]() AOBO+
AOBO+![]() BC2=
BC2=![]() b2+b+1,(0<b<2).
b2+b+1,(0<b<2).
(2)①结论:FA=FB,FA⊥FB,理由如下:
如图,
作FG⊥y轴,FH⊥x轴垂足分别为G、H.
∵A(0,a)向右平移a个单位到D,
∴点D坐标为(a,a),点E坐标为(a+b,0),
∴∠DOE=45°,
∵EF⊥OD,
∴∠OFE=90°∠FOE=∠FEO=45°,
∴FO=EF,
∴FH=OH=HE=![]() (a+b),
(a+b),
∴点F坐标(![]() ,
,![]() ),
),
∴FG=FH,四边形FHOG是正方形,
∴OG=FH=![]() ,∠GFH=90°,
,∠GFH=90°,
∴AG=AO﹣OG=a﹣![]() =
=![]() ,BH=OH﹣OB=
,BH=OH﹣OB=![]() -b=
-b=![]() ,
,
∴AG=BH,
在△FGA和△FHB中, ,
,
∴△FGA≌△FHB,
∴FA=FB,∠AFG=∠BFH,
∴∠AFB=∠GFH=90°.
AF⊥BF,AF=BF.
②∵△FGA≌△FHB,
∴∠FBH=∠OAF,
在RT△BFH中,∵BF=OA﹣OB=a﹣b,BH=![]() ,
,
∴cos∠FBH=![]() ,
,
∴∠FBH=60°,
∴∠OAF=60°.
故答案为60°.
【解析】(1)①化简得(a﹣2)2+(b﹣1)2=0,根据非负数的性质即可求出a、b.②利用S四边形AOBC=S△AOB+S△ABC即可解决.
(2)①结论:AF=FB,AF⊥FB,作FG⊥y轴,FH⊥x轴垂足分别为G、H.,先证明四边形FHOG是正方形,然后证明△FGA≌△FHB得FA=FB,∠AFG=∠BFH所以∠AFB=∠GFH=90°.从而得证.
②由△FGA≌△FHB得∠FBH=∠OAF,在RT△FBH中,求出cos∠FBH=![]() 的值即可解决.
的值即可解决.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:5x2﹣[4x2﹣(2x﹣1)﹣3x];其中x=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表为某乡村100名居民的年龄分布情况(每组含最小值,不含最大值):
年龄
0~10
10~20
20~30
30~40
40~50
50~60
60~70
70~80
80~90
人数
8
10
12
12
14
19
13
7
5
如果老人以60岁为标准,那么该村老人所占的比例约是 ________%.
-
科目: 来源: 题型:
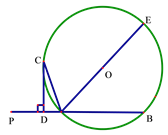
查看答案和解析>>【题目】已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D
(1)求证:CD为⊙O的切线
(2)若DC+DA=6,⊙O的直径为10,求AB的长度。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中的不可能事件是( )
A.通常加热到100℃时,水沸腾
B.抛掷2枚正方体骰子,都是6点朝上
C.经过有交通信号灯的路口,遇到红灯
D.任意画一个三角形,其内角和是360° -
科目: 来源: 题型:
查看答案和解析>>【题目】下列性质中,等腰三角形具有而直角三角形不一定具有的是( )
A.任意两边之和大于第三边
B.有一个角的平分线垂直于这个角的对边
C.至少有两个角是锐角
D.内角和等于180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】9的平方根是 .
相关试题

