【题目】如图1,在△ABC中,∠BAC=90°,AB=AC.MN是过点A的直线,BD⊥MN 于D,CE⊥MN于E.
(1)求证:BD=AE.
(2)若将MN绕点A旋转,使MN与BC相交于点G(如图2),其他条件不变,求证:BD=AE.
(3)在(2)的情况下,若CE的延长线过AB的中点F(如图3),连接GF,求证:∠AFE=∠BFG.

参考答案:
【答案】(1)证明见详解;(2)证明见详解;(3)证明见详解.
【解析】
(1)首先证明∠1=∠3,再证明△ADB≌△CEA,然后根据全等三角形的性质可得BD=AE;
(2)首先证明∠BAD=∠ACE,再证明△ABD≌△CAE,根据全等三角形对应边相等可得BD=AE;
(3)首先证明△ACF≌△BAP,然后再证明△BFG≌△BPG,再根据全等三角形对应角相等可得∠BPG=∠BFG,再根据等量代换可得结论∠BFG=∠AFE.
证明:(1)如图,
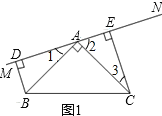
∵BD⊥MN,CE⊥MN,
∴∠BDA=∠AEC=90°,
∵∠BAC=90°,
∴∠1+∠2=90°,
又∵∠3+∠2=90°,
∴∠1=∠3,
在△ADB和△CEA中, ,
,
∴△ADB≌△CEA(AAS),
∴BD=AE;
(2)如图,

∵BD⊥MN,CE⊥MN,
∴∠BDA=∠CEA=90°,
∵∠BAD+∠CAE=90°,∠ACE+∠CAE=90°,
∴∠BAD=∠ACE,
在△ABD和△CAE中,

∴△ABD≌△CAE(AAS),
∴BD=AE;
(3)过B作BP∥AC交MN于P,
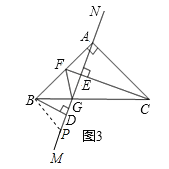
∵BP∥AC,
∴∠PBA+∠BAC=180°,
∵∠BAC=90°,
∴∠PBA=∠BAC=90°,
由(2)得:∠BAP=∠ACF,
∴在△ACF和△BAP中,
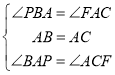
∴△ACF≌△BAP(ASA),
∴∠AFC=∠BPA,AF=BP
∵BF=AF,
∴BF=BP,
∵△ABC是等腰直角三角形,
∴∠ABC=45°,
又∵∠PBA=90°,
∴∠PBG=45°,
∴∠ABC=∠PBG,
在△BFG和△BPG中,
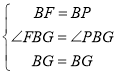
∴△BFG≌△BPG(SAS),
∴∠BPG=∠BFG,
∵∠BPG=∠AFE,
∴∠BFG=∠AFE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了备战初三物理、化学实验操作考试,某校对初三学生进行了模拟训练.物理、化学各有3个不同的操作实验题目,物理用番号①、②、③代表,化学用字母a、b、c表示.测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定.
(1)小张同学对物理的①、②和化学的b、c实验准备得较好.请用树形图或列表法求他两科都抽到准备得较好的实验题目的概率;
(2)小明同学对物理的①、②、③和化学的a实验准备得较好.他两科都抽到准备得较好的实验题目的概率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】“8字”的性质及应用:
(1)如图①,AD、BC相交于点O,得到一个“8字”ABCD,求证:∠A+∠B=∠C+∠D.
(2)图②中共有多少个“8字”?
(3)如图②,∠ABC和∠ADC的平分线相交于点E,利用(1)中的结论证明∠E=
 (∠A+∠C).
(∠A+∠C).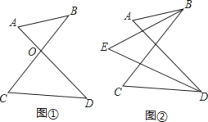
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在3×3的正方形网格中标出了∠1和∠2.则∠1+∠2= .
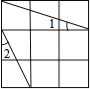
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直线
 上依次摆放着七个正方形(如图所示),已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是
上依次摆放着七个正方形(如图所示),已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是 ,则
,则 _______.
_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中每个小正方形边长都是1.
(1)画出△ABC关于直线1对称的图形△A1BlCl;
(2)在直线l上找一点P,使PB=PC;(要求在直线1上标出点P的位置)
(3)连接PA、PC,计算四边形PABC的面积.

相关试题

