【题目】如图,在平面直角坐标系![]() 中,双曲线
中,双曲线![]() =
=![]() 经过□
经过□![]() 的顶点
的顶点![]() 、
、![]() ,点
,点![]() 的坐标为(
的坐标为(![]() ,
,![]() 1),点
1),点![]() 在
在![]() 轴上,且
轴上,且![]() ∥
∥![]() 轴,平行四边形
轴,平行四边形![]() 的面积是8.
的面积是8.
(1)求双曲线和AB所在直线的解析式;
(2)点![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )是双曲线
)是双曲线![]() =
=![]() (
(![]() <0)图象上的两点,若
<0)图象上的两点,若![]() >
>![]() ,则
,则![]()
![]() ;(填“<”、“=”或“>”)
;(填“<”、“=”或“>”)

参考答案:
【答案】(1)![]() ,y=6x-1;(2)<.
,y=6x-1;(2)<.
【解析】
(1)D点直接代入反比例函数即可得到反比例函数解析式,由平行四边形性质可得到A、B两点坐标,然后代入一次函数解析式,即可解得一次函数解析式 (2)利用反比例函数性质可直接得到结果
(1)D点坐标为(-2,-1)直接代入反比例函数解析式,得到k=2,即反比例函数解析式为![]() ;因为
;因为![]() ∥
∥![]() 轴,所以A点坐标为(0,-1),又因为平行四边形的面积为8,AD=2,所以平行四边形的高为4,得到B点纵坐标为3,B点又在反比例函数上,代入函数得到x=
轴,所以A点坐标为(0,-1),又因为平行四边形的面积为8,AD=2,所以平行四边形的高为4,得到B点纵坐标为3,B点又在反比例函数上,代入函数得到x=![]() ,所以B点坐标为(
,所以B点坐标为(![]() ,3);设直线AB的函数解析式为y=kx+b,将A(0,-1),B(
,3);设直线AB的函数解析式为y=kx+b,将A(0,-1),B(![]() ,3)代入一次函数解析式得到方程0=-k+b,3=
,3)代入一次函数解析式得到方程0=-k+b,3=![]() k+b,解两个方程得到k=6,b=-1,所以一次函数解析式为y=6x-1
k+b,解两个方程得到k=6,b=-1,所以一次函数解析式为y=6x-1
故双曲线解析式为![]() ,直线AB的解析式为y=6x-1
,直线AB的解析式为y=6x-1
(2)利用反比例函数性质,当k>0,x<0时,y随x增大而减小,因为![]() >
>![]() ,所以
,所以![]() <
<![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】将若干个奇数按每行8个数排成如图的形式:
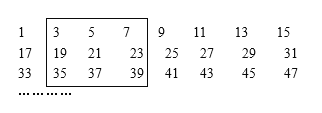
小军画了一方框框住了其中的9个数.
(1)如图中方框内9个数之和是 ;
(2)若小军画的方框内9个数之和等于333,则这个方框内左下角的那个数为_________;
(3)试说明:方框内的9个数之和总是9的倍数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在∠A(0°<∠A<90°)的内部画线段,并使线段的两端点分别落在角的两边AB、AC上,如图所示,从点A1开始,依次向右画线段,使线段与线段在两端点处互相垂直,A1A2为第1条线段.设AA1=A1A2=A2A3=1,则∠A =_____
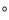 ;若记线段A2n-1A2n的长度为an(n为正整数),如A1A2=a1,A3A4=a2,则此时a2=_______,an=________(用含n的式子表示).
;若记线段A2n-1A2n的长度为an(n为正整数),如A1A2=a1,A3A4=a2,则此时a2=_______,an=________(用含n的式子表示).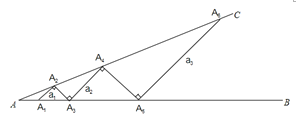
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,已知⊙O的直径为AB,AC⊥AB于点A, BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.下面四个结论:①ED是⊙O的切线;②BC=2OE③△BOD为等边三角形;④△EOD ∽ △CAD,正确的是( )

A. ①② B. ②④ C. ①②④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以AD为直径的半圆经过点E、B,点E、B是半圆的三等分点,弧 BE的长为
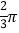 ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )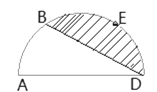
A.
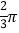 B.
B. 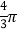 C.
C. 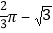 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
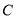 ,线段
,线段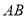 .
.(1)如图,若点
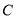 在线段
在线段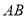 上,且
上,且 ,
, ,点
,点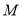 、
、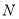 分别是
分别是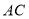 、
、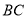 的中点,则线段
的中点,则线段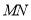 的长度是 ;
的长度是 ;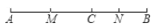
(2)若把(1)中点
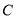 在线段
在线段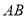 上,且
上,且 ,
, ,改为点
,改为点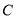 是线段
是线段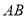 上任意一点,且
上任意一点,且 ,
,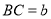 ,其他条件不变,请求出线段
,其他条件不变,请求出线段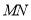 的长度(用含
的长度(用含 、
、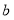 的式子表示);
的式子表示);(3)若把(2)中点
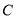 是线段
是线段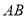 上任意一点,改为点
上任意一点,改为点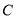 是直线
是直线 上任意一点,其他条件不变,则线段
上任意一点,其他条件不变,则线段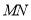 的长度会变化吗?若有变化,求出结果.
的长度会变化吗?若有变化,求出结果. -
科目: 来源: 题型:
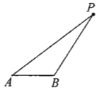
查看答案和解析>>【题目】如图,分别过点P作直线AB的垂线
(1)
 (2)
(2)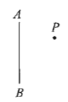
(3)
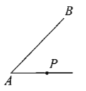 (4)
(4)
相关试题

