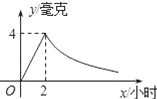
【题目】病人按规定的剂量服用某种药物,测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克,已知服药后,2小时前每毫升血液中的含药量y(毫克)与时间x(小时)成正比例,2小时后y与x成反比例(如图所示).根据以上信息解答下列问题.
(1)求当0≤x≤2时,y与x的函数关系式;
(2)求当x>2时,y与x的函数关系式;
(3)若每毫升血液中的含药量不低于2毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?
参考答案:
【答案】(1)y=2x;(2)![]() (3)3小时
(3)3小时
【解析】分析:(1)根据点(2,4)利用待定系数法求正比例函数解形式;(2)根据点(2,4)利用待定系数法求反比例函数解形式;(3)根据两函数解析式求出函数值是2时的自变量的值,即可求出有效时间.
本题解析:(1)根据图象,正比例函数图象经过点(2,4),
设函数解析式为y=kx,则2k=4,解得k=2,
所以函数关系为y=2x(0x2);
(2)根据图象,反比例函数图象经过点(2,4),
设函数解析式为y=![]() ,则
,则![]() =4,解得k=8,所以,函数关系为y=8x(x>2);
=4,解得k=8,所以,函数关系为y=8x(x>2);
(3)当y=2时,2x=2,解得x=1, ![]() =2,解得x=4,41=3小时,
=2,解得x=4,41=3小时,
∴服药一次,治疗疾病的有效时间是3小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=2x2-8x+1的最小值是___________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A坐标为(6,0),在B在y轴的正半轴上,且S△AOB=24.
(1)求点B坐标;
(2)若点P从B出发沿y轴负半轴运动,速度每秒2个单位,运动时间t秒,△AOP的面积为S,求S与t的关系式,并直接写出t的取值范围;
(3)在(2)的条件下,若S△AOP:S△ABP=1:3,且S△AOP+S△ABP=S△AOB , 在线段AB的垂直平分线上是否存在点Q,使得△AOQ的面积与△BPQ的面积相等?若存在,求出Q点坐标;若不存在,请说明理由.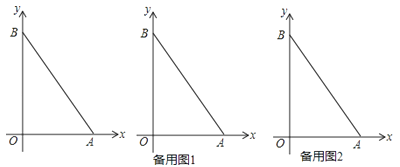
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列各数填在相应的集合里.
﹣3.8,﹣10,4.3,﹣|﹣ |,42 , 0,﹣(﹣
|,42 , 0,﹣(﹣ 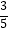 )
)
整数集合:{ …};
分数集合:{ …};
正数集合:{ …};
负数集合:{ …}. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)[(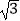 )2﹣|﹣2|]×(﹣3)
)2﹣|﹣2|]×(﹣3)
(2)(﹣1)2014﹣|﹣6|+(π﹣50)0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件,为了迎接“双11”节,扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件。
(1)降价前商场每月销售该商品的利润是多少元?
(2)要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果把收入30元记作+30元,那么支出20元可记作 .
相关试题

