【题目】⑴ 阅读理解:我们知道在直角三角形中,有无数组勾股数,例如:5、12、13;9、40、41;……但其中也有一些特殊的勾股数,例如:3、4、5;是三个连续正整数组成的勾股数.
解决问题:① 在无数组勾股数中,是否存在三个连续偶数能组成勾股数?
答: ,若存在,试写出一组勾股数: .
② 在无数组勾股数中,是否还存在其它的三个连续正整数能组成勾股数?若存在,求出勾股数,若不存在,说明理由.
③ 在无数组勾股数中,是否存在三个连续奇数能组成勾股数?若存在,求出勾股数,若不存在,说明理由.
⑵ 探索升华:是否存在锐角△ABC三边也为连续正整数;且同时还满足:∠B>∠C>∠A;∠ABC=2∠BAC?若存在,求出△ABC三边的长;若不存在,说明理由.
参考答案:
【答案】(1)①存在,6、8、10;②不存在,理由见解析;③不存在,理由见解析;(2)存在.三边长分别是4、5、6
【解析】分析:(1)①3,4,5是连续正整数,则它们的2倍是连续偶数;②设三个连续正整数分别是:n-1,n,n+1(n>1的整数),用勾股定理列方程求解;③设三个连续奇数分别是:2n-1,2n+1,2n+3(n>1的整数),由奇数的平方是奇数,奇数+奇数=偶数分析判断;(2)延长CB到点D,使BD=BA,连接AD,证明△CAB∽△CDA,用比例线段列方程求解.
详解:⑴①答:存在;6,8,10.
②答:不存在.
理由:假设在无数组勾股数中,还存在其它的三个连续正整数能组成勾股数.
设三个连续正整数分别是:n-1,n,n+1(n>1的整数),
则:(n-1)2+n2=(n+1)2,
得:n1=4,n2=0(舍去)
∴当n=4时,n-1=3,n+1=5,
∴三个连续正整数仍然为3,4,5,
∴不存在其它的三个连续正整数能组成勾股数.
③答:不存在.
理由:假设在无数组勾股数中,存在三个连续奇数能组成勾股数.
设三个连续奇数分别是:2n-1,2n+1,2n+3(n>1的整数),
∵(奇数)2+(奇数)2≠(奇数)2
∴不存在三个连续奇数能组成勾股数.
⑵答:存在.三边长分别是4,5,6.
理由:如图,在△ABC中,设AB=x,AC=x+1,BC=x-1(x>1的整数),
则:∠B>∠C>∠A;且∠ABC=2∠BAC,
延长CB到点D,使BD=BA,连接AD.
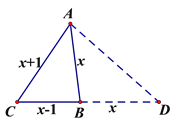
∴∠BAD=∠BDA,
又∵∠ABC=∠BAD+∠BDA=2∠BDA,且∠ABC=2∠BAC,
∴∠BAC=∠BDA.
又∵∠C=∠C,∴△CAB∽△CDA,
∴AC2=BC·DC,∴(x+1)2=(x-1)[(x-1)+x],
得:x1=5,x2=0(舍去).
当x=5时,x-1=4,x+1=6,即:BC=4,AB=5,AC=6,
答:存在锐角△ABC三边为连续正整数,BC=4,AB=5,AC=6;
且同时还满足:∠B>∠C>∠A;∠ABC=2∠BAC.
-
科目: 来源: 题型:
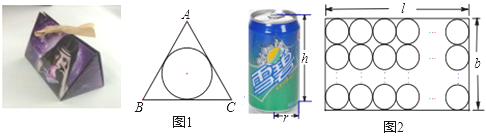
查看答案和解析>>【题目】(1)如图1是一家唇膏卖家的礼品装,卖家采用了正三梭柱形盒子,里面刚好横放一支圆柱形唇膏,右图是其横载面,△ABC为正三角形.求这个包装盒空间的最大利用率(圆柱体积和纸盒容积的比);
(2)一个长宽高分别为l,b.h的长方体纸箱装满了一层高为h的圆柱形易拉罐如图2.求纸箱空间的利用率(易拉罐总体积和纸箱容积的比);
(3)比较上述两种包装方式的空间利用率哪个大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( )

A.
B.
C.

D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A. 若a2=b2,则a=b B. 若∠1+∠2=90,则∠1与∠2互余
C. 若∠α与∠β是同位角,则∠α=∠β D. 若a⊥b,b⊥c,则a⊥c
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=
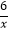 在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( ) 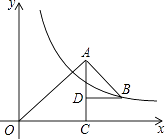
A.36
B.12
C.6
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC是正三角形,曲线CDEF叫做“正三角形的渐开线”,其中
 、
、  、
、  圆心依次按A、B、C…循环,它们依次相连接.若AB=1,则曲线CDEF长是(结果保留π).
圆心依次按A、B、C…循环,它们依次相连接.若AB=1,则曲线CDEF长是(结果保留π). 
相关试题

