【题目】a,b是有理数,它们在数轴上的对应点的位置如图所示:把a,﹣a,b,﹣b按照从小到大的顺序排列( ) ![]()
A.﹣b<﹣a<a<b
B.a<﹣b<b<﹣a
C.﹣b<a<﹣a<b
D.a<﹣b<﹣a<b
参考答案:
【答案】B
【解析】解:因为从数轴可知:a<0<b,|a|>|b|, 所以a<﹣b<b<﹣a,
故选B.
【考点精析】根据题目的已知条件,利用数轴和有理数大小比较的相关知识可以得到问题的答案,需要掌握数轴是规定了原点、正方向、单位长度的一条直线;有理数比大小:1、正数的绝对值越大,这个数越大2、正数永远比0大,负数永远比0小3、正数大于一切负数4、两个负数比大小,绝对值大的反而小5、数轴上的两个数,右边的数总比左边的数大6、大数-小数 > 0,小数-大数 < 0.
-
科目: 来源: 题型:
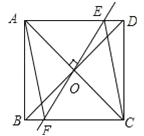
查看答案和解析>>【题目】如图,矩形ABCD中,对角线AC和BD相交于点O,过O作EF⊥AC,交AD于E,交BC于F,连接AF、CE.
(1)求证:四边形AECF是菱形;
(2)若AB=3,BC=4,求菱形AECF的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列不等式或等式组:
(1)10﹣3(x+5)≤1
(2)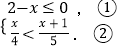 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】若一个角的补角等于它的余角4倍,则这个角的度数是度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(14,0)、(14,3)、(4,3).点P、Q同时从原点出发,分别作匀速运动,其中点P沿OA向终点A运动,速度为每秒1个单位;点Q沿OC、CB向终点B运动,当这两点中有一点到达自己的终点时,另一点也停止运动.设P从出发起运动了t秒.
(1)如果点Q的速度为每秒2个单位,①试分别写出这时点Q在OC上或在CB上时的坐标(用含t的代数式表示,不要求写出t的取值范围);
②求t为何值时,PQ∥OC?
(2)如果点P与点Q所经过的路程之和恰好为梯形OABC的周长的一半,①试用含t的代数式表示这时点Q所经过的路程和它的速度;
②试问:这时直线PQ是否可能同时把梯形OABC的面积也分成相等的两部分?如有可能,求出相应的t的值和P、Q的坐标;如不可能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式:
 并在数轴上表示出它的解集.
并在数轴上表示出它的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b,当x=2时y的值是﹣1,当x=﹣1时y的值是5.
(1)求此一次函数的解析式;
(2)若点P(m,n)是此函数图象上的一点,﹣3≤m≤2,求n的最大值.
相关试题

