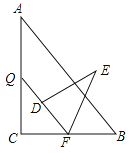
【题目】如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
(1)求证:PQ∥AB;
(2)若点D在∠BAC的平分线上,求CP的长;
(3)若△PDE与△ABC重叠部分图形的周长为T,且12≤T≤16,求x的取值范围.
参考答案:
【答案】(1)证明见试题解析;(2)6;(3)1≤x≤![]() .
.
【解析】
试题分析:(1)先由勾股定理求出AC的长,再由相似三角形的判定定理得出△PQC∽△BAC,得出∠CPQ=∠B,由此可得出结论;
(2)连接AD,由PQ∥AB可得∠ADQ=∠DAB,再由点D在∠BAC的平分线上,得到∠DAQ=∠DAB,故∠ADQ=∠DAQ,AQ=DQ.在Rt△CPQ中根据勾股定理可知,AQ=12﹣4x,故可得出x的值,进而得出结论;
(3)当点E在AB上时,根据等腰三角形的性质求出x的值,再分0<x≤![]() ;
;![]() <x<3两种情况进行分类讨论.
<x<3两种情况进行分类讨论.
试题解析:(1)∵在Rt△ABC中,AB=15,BC=9,∴AC=![]() =
=![]() =12.∵
=12.∵![]() ,
,![]() ,∴
,∴![]() .∵∠C=∠C,∴△PQC∽△BAC,∴∠CPQ=∠B,∴PQ∥AB;
.∵∠C=∠C,∴△PQC∽△BAC,∴∠CPQ=∠B,∴PQ∥AB;
(2)连接AD,∵PQ∥AB,∴∠ADQ=∠DAB,∵点D在∠BAC的平分线上,∴∠DAQ=∠DAB,∴∠ADQ=∠DAQ,∴AQ=DQ,在Rt△CPQ中,PQ=5x,∵PD=PC=3x,∴DQ=2x.∵AQ=12﹣4x,∴12﹣4x=2x,解得x=2,∴CP=3x=6;
(3)当点E在AB上时,∵PQ∥AB,∴∠DPE=∠PEB.∵∠CPQ=∠DPE,∠CPQ=∠B,∴∠B=∠PEB,∴PB=PE=5x,∴3x+5x=9,解得x=![]() .
.
①当0<x≤![]() 时,T=PD+DE+PE=3x+4x+5x=12x,此时0<T≤
时,T=PD+DE+PE=3x+4x+5x=12x,此时0<T≤![]() ;
;
②当![]() <x<3时,设PE交AB于点G,DE交AB于F,作GH⊥FQ,垂足为H,∴HG=DF,FG=DH,Rt△PHG∽Rt△PDE,∴
<x<3时,设PE交AB于点G,DE交AB于F,作GH⊥FQ,垂足为H,∴HG=DF,FG=DH,Rt△PHG∽Rt△PDE,∴![]() ,∵PG=PB=9﹣3x,∴
,∵PG=PB=9﹣3x,∴![]() ,∴GH=
,∴GH=![]() (9﹣3x),PH=
(9﹣3x),PH=![]() (9﹣3x),∴FG=DH=3x﹣
(9﹣3x),∴FG=DH=3x﹣![]() (9﹣3x),∴T=PG+PD+DF+FG=(9﹣3x)+3x+
(9﹣3x),∴T=PG+PD+DF+FG=(9﹣3x)+3x+![]() (9﹣3x)+[3x﹣
(9﹣3x)+[3x﹣![]() (9﹣3x)]=
(9﹣3x)]=![]() ,此时,
,此时,![]() <T<18.∴当0<x<3时,T随x的增大而增大,∴T=12时,即12x=12,解得x=1;TA=16时,即
<T<18.∴当0<x<3时,T随x的增大而增大,∴T=12时,即12x=12,解得x=1;TA=16时,即![]() =16,解得x=
=16,解得x=![]() .∵12≤T≤16,∴x的取值范围是1≤x≤
.∵12≤T≤16,∴x的取值范围是1≤x≤![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的三边分别为a、b、c,且(a-b)2+(a2+b2-c2)2=0,则三角形的形状为————————————————。
-
科目: 来源: 题型:
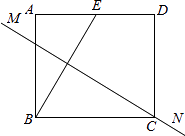
查看答案和解析>>【题目】如图,矩形纸片ABCD中,点E是AD的中点,且AE=1,BE的垂直平分线MN恰好过点C.则矩形的一边AB的长度为( )
A.1
B.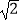
C.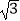
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( )
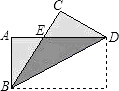
A.△EBD是等腰三角形,EB=ED
B.折叠后∠ABE和∠CBD一定相等
C.折叠后得到的图形是轴对称图形
D.△EBA和△EDC一定是全等三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )

A.12
B.24
C.12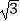
D.16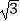
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为( )
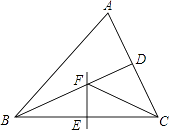
A.48°
B.36°
C.30°
D.24° -
科目: 来源: 题型:
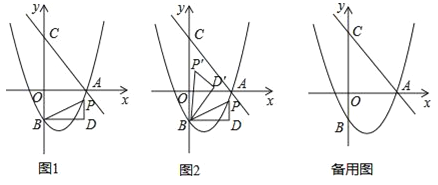
查看答案和解析>>【题目】如图1,直线
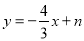 交x轴于点A,交y轴于点C(0,4),抛物线
交x轴于点A,交y轴于点C(0,4),抛物线 经过点A,交y轴于点B(0,﹣2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为m.
经过点A,交y轴于点B(0,﹣2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为m.(1)求抛物线的解析式;
(2)当△BDP为等腰直角三角形时,求线段PD的长;
(3)如图2,将△BDP绕点B逆时针旋转,得到△BD′P′,且旋转角∠PBP′=∠OAC,当点P的对应点P′落在坐标轴上时,请直接写出点P的坐标.
相关试题

