搜索
【题目】如图，要在长方形和环形地块中铺设草坪，长方形的长、宽分别为a m、b m，环形的外圆、内圆的半径分别为R m、r m．
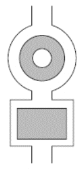
(1)求共需草皮的面积．
(2)若草皮每平方米需30元，当
时，求草皮的费用.(保留π)
参考答案：
【答案】(1) 
；(2) （600+210
）元．
【解析】
（1）分别表示出长方形地块和环形地块中铺设草皮的面积，再相加即可；
（2）把相关数据代入（1）中的代数式进行计算得出铺设草皮的面积，根据草皮每平方米需30元，即可得出答案．
解：（1）根据题意得：
长方形地块中铺设草皮的面积为：ab
，
环形地块中铺设草皮的面积为：
，
∴共需草皮的面积为：；
（2）当
时，
=
=（20+7），
草皮的费用为：30×（20+7）=（600+210）元．
-
科目： 来源： 题型：
查看答案和解析>>【题目】用同样大小的两种不同颜色的正方形纸片，按图的方式拼正方形.
(1)第①个图形中有1个小正方形，第②个图形中有4个小正方形，第③个图形中有9个小正方形，第⑦个图形中有__________个小正方形.
(2)第⑩个图形比第⑨个图形多_________个小正方形.
(3)第n个图形比第n-1个图形多_________个小正方形.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口的直径 EF 长为10cm,母线OE(OF)长为10cm,在母线OF 上的点A 处有一块爆米花残渣且FA＝2cm,一只蚂蚁从杯口的点E 处沿圆锥表面爬行到A 点,则此蚂蚁爬行的最短距离为 cm．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一条笔直的公路上有A、B、C三地，C地位于A、B两地之间，甲车从A地沿这条公路匀速驶向C地，乙车从B地沿这条公路匀速驶向A地，在甲车出发至甲车到达C地的过程中，甲、乙两车各自与C地的距离y（km）与甲车行驶时间t（h）之间的函数关系如图所示．下列结论：①甲车出发2h时，两车相遇；②乙车出发1.5h时，两车相距170km；③乙车出发
h时，两车相遇；④甲车到达C地时，两车相距40km．其中正确的是______（填写所有正确结论的序号）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】A、B、C、D四个车站的位置如图所示：
(1)求A、D两站的距离；
(2)求C、D两站的距离；
(3)比较A、C两站的距离与B、D两站的距离，哪两站的距离更大？大多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1是一个长为
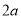、宽为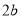
的长方形（其中
，
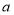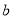均为正数，且
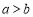），沿图中虚线用剪刀均匀分成四块相同小长方形，然后按图2方式拼成一个大正方形.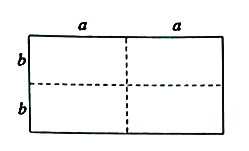
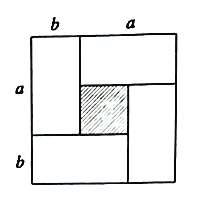
图1 图2
（1）图2中大正方形的边长为 ；小正方形（阴影部分）的边长为 .（用含
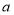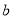、的代数式表示）（2）仔细观察图2，请你写出下列三个代数式：
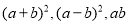所表示的图形面积之间的相等关系，并选取适合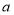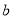，的数值加以验证.（3）已知
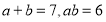.则代数式
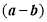的值为 . -
科目： 来源： 题型：
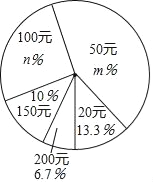
查看答案和解析>>【题目】某中学在一次爱心捐款活动中，全体同学积极踊跃捐款．现抽查了九年级（1）班全班同学捐款情况，并绘制出如下的统计表和统计图：
捐款（元）
20
50
100
150
200
人数（人）
4
12
9
3
2
求：（Ⅰ）m=_____，n=_____；
（Ⅱ）求学生捐款数目的众数、中位数和平均数；
（Ⅲ）若该校有学生2500人，估计该校学生共捐款多少元？
相关试题
