【题目】函数y=kx﹣2中,y随x的增大而减小,则它的图像可以是( )
A.
B.
C.
D.
参考答案:
【答案】D
【解析】解:∵函数y=kx﹣2中,y随x的增大而减小,
∴k<0,
∴图像一定过二、四象限,
∵b=﹣2,
∴图像与y轴的交点在x轴下方.
故选:D.
【考点精析】根据题目的已知条件,利用一次函数的性质和一次函数的图象和性质的相关知识可以得到问题的答案,需要掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).
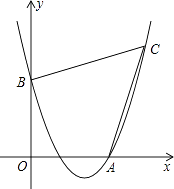
(1)求抛物线的表达式;
(2)证明:四边形AOBC的两条对角线互相垂直;
(3)在四边形AOBC的内部能否截出面积最大的DEFG?(顶点D,E,F,G分别在线段AO,OB,BC,CA上,且不与四边形AOBC的顶点重合)若能,求出DEFG的最大面积,并求出此时点D的坐标;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t s,解答下列问题:
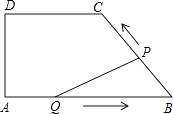
(1)当t为何值时,P,Q两点同时停止运动?
(2)设△PQB的面积为S,当t为何值时,S取得最大值,并求出最大值;
(3)当△PQB为等腰三角形时,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b(k≠0)的图象与x轴的交点坐标为(-2,0),则下列说法:①y随x的增大而减小;②关于x的方程kx+b=0的解为x=-2;③kx+b>0的解集是x>-2;④b<0.其中正确的有__________.(填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度hcm,则h的取值范围是( )

A.h≤17cm
B.h≥8cm
C.15cm≤h≤16cm
D.7cm≤h≤16cm -
科目: 来源: 题型:
查看答案和解析>>【题目】探索与证明:(1)如图1,直线m经过正三角形ABC的顶点A,在直线m上取两点 D,E,使得∠ADB=60°,∠AEC=60°.通过观察或测量,猜想线段BD,CE与DE之间满足的数量关系,并予以证明;
(2)将(1)中的直线m绕点A逆时针方向旋转一个角度到如图2的位置,并使∠ADB=120°,∠AEC=120°.通过观察或测量,请直接写出线段BD,CE与DE之间满足的数量关系.
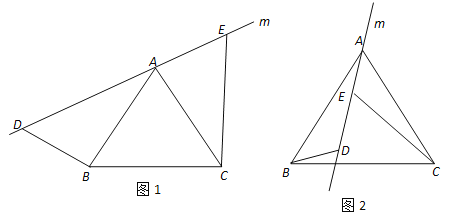
-
科目: 来源: 题型:
查看答案和解析>>【题目】[动手操作] 如图所示,地面全是用正三角形的材料铺设而成的.
(1)用这种形状的材料为什么能铺成平整、无缝隙的地面?
(2)像上面那样铺地砖,能否全用正十边形的材料?为什么?
(3)你能不能另外想出用一种相同的正多边形材料铺地面的方案?并画出草图.

相关试题

