【题目】二次函数![]() 的图象的对称轴是直线
的图象的对称轴是直线![]() ,其图象的一部分如图所示则:①
,其图象的一部分如图所示则:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤当
;⑤当![]() 时,
时,![]() .其中判断正确的有( )个.
.其中判断正确的有( )个.

A. 2 B. 3 C. 4 D. 5
参考答案:
【答案】C
【解析】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴判定b与0的关系以及2a+b=0;当x=-1时,y=a-b+c;然后由图象确定当x取何值时,y>0.
解:①∵开口向下,
∴a<0,
∵对称轴在y轴右侧,
∴-![]() >0,
>0,
∴b>0,
∵抛物线与y轴交于正半轴,
∴c>0,
∴abc<0,故正确;
②∵对称轴为直线x=1,抛物线与x轴的一个交点横坐标在2与3之间,
∴另一个交点的横坐标在0与-1之间;
∴当x=-1时,y=a-b+c<0,故正确;
③∵对称轴x=-![]() =1,
=1,
∴2a+b=0;故正确;
④∵2a+b=0,
∴b=-2a,
∵当x=-1时,y=a-b+c<0,
∴a-(-2a)+c=3a+c<0,故正确;
⑤如图,当-1<x<3时,y不只是大于0.故错误.
∴正确的有4个.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
 的图象经过点
的图象经过点 和
和 ,下列关于此二次函数的叙述,正确的是( )
,下列关于此二次函数的叙述,正确的是( )
A. 当
 时,
时, 的值小于
的值小于
B. 当
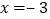 时,
时, 的值大于
的值大于
C. 当
 时,
时, 的值等于
的值等于
D. 当
 时,
时, 的值大于
的值大于
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,AD是BC边上的高,点E是AC边的中点,点P是AD上的一个动点,当PC+PE最小时,∠CPE的度数是( )

A.30°B.45°C.60°D.70°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形;
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示为二次函数
 的图象,在下列选项中错误的是( )
的图象,在下列选项中错误的是( )
A.

B.
 时,
时, 随
随 的增大而增大
的增大而增大C.

D. 方程
 的根是
的根是 ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系xOy中的线段AB及点P,给出如下定义:
若点P满足PA=PB,则称P为线段AB的“轴点”,其中,当0°<∠APB<60°时,称P为线段AB的“远轴点”;当60°≤∠APB≤180°时,称P为线段AB的“近轴点”.
(1)如图1,点A,B的坐标分别为(-2,0),(2,0),则在
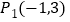 ,
, ,
, ,
, 中,线段AB的“近轴点”是 .
中,线段AB的“近轴点”是 .(2)如图2,点A的坐标为(3,0),点B在y轴正半轴上,且∠OAB=30°.
①若P为线段AB的“远轴点”,直接写出点P的横坐标t的取值范围 ;
②点C为y轴上的动点(不与点B重合且BC≠AB),若Q为线段AB的“轴点”,当线段QB与QC的和最小时,求点Q的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC是等腰直角三角形,其中∠C=90°,AC=BC. D是BC上任意一点(点D与点B,C都不重合),连接AD,CF⊥AD,交AD于点E,交AB于点F,BG⊥BC交CF的延长线于点G.

(1)依题意补全图形,并写出与BG相等的线段.
(2)当点D为线段BC中点时,连接DF .求证:∠BDF=∠CDE.
(3)当点C和点F关于直线AD成轴对称时,直接写出线段CE,DE,AD三者之间的数量关系.
相关试题

