【题目】△ABC是等腰直角三角形,其中∠C=90°,AC=BC. D是BC上任意一点(点D与点B,C都不重合),连接AD,CF⊥AD,交AD于点E,交AB于点F,BG⊥BC交CF的延长线于点G.

(1)依题意补全图形,并写出与BG相等的线段.
(2)当点D为线段BC中点时,连接DF .求证:∠BDF=∠CDE.
(3)当点C和点F关于直线AD成轴对称时,直接写出线段CE,DE,AD三者之间的数量关系.
参考答案:
【答案】(1)![]() .(2)证明过程见解答.(3)
.(2)证明过程见解答.(3)![]() .
.
【解析】
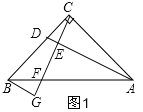
(1)如图1,根据ASA证明△CBG≌△ACD,得BG=DC;
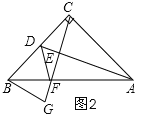
(2)如图2,由(1)得:△CBG≌△ACD,得∠CDE=∠G,再证明△BDF≌△BGF得出结论;
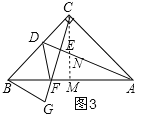
(3)如图3,作辅助线,分别证明△ACD≌△AFD和△ACN≌△CBF,得DN=2DE,AN=CF=2CE,可以得出结论.
解:(1)BG=DC,理由是:
如图1,∵∠ACB=90°,
∴∠BCG+∠GCA=90°,
∵CF⊥AD,
∴∠CEA=90°,
∴∠GCA+∠CAD=90°,
∴∠BCG=∠CAD,
∵∠ACB=∠CBG=90°,AC=BC,
∴△CBG≌△ACD(ASA),
∴BG=DC;
(2)如图2,由(1)得:△CBG≌△ACD,
∴∠CDE=∠G,
∵D是BC的中点,
∴BD=DC,
∵BG=DC,
∴BG=BD,
∵∠ACB=90°,AC=BC,
∴∠CBA=45°,
∵∠CBG=90°,
∴∠GBA=45°,
∴∠GBA=∠CBA=45°,
∵BF=BF,
∴△BDF≌△BGF(SAS),
∴∠BDF=∠G,
∴∠BDF=∠CDE;
(3)AD=2DE+2CE,理由是:
如图3,过C作CM⊥AB于M,交AD于N,
∵AC=BC,∠ACB=90°,
∴∠BCM=∠ACM=45°,
∵点C和点F关于直线AD成轴对称,
∴AD是CF的中垂线,
∴CE=EF,CD=DF,AC=AF,
∵AD=AD,
∴△ACD≌△AFD,
∴∠DFA=∠ACB=90°,
∵∠CBA=45°,
∴△DBF是等腰直角三角形,
∴BF=DF,
∴BF=DF=CD,
∵AC=AF,∠BAC=45°,
∴∠ACF=∠CFA=67.5°,∠CAE=∠FAE=22.5°,
∴∠BCG=90°-67.5°=22.5°,
∴∠ECN=45°-22.5°=22.5°,
∴∠ECN=∠BCG,
∴△DCE≌△NCE,
∴DC=CN,DE=EN,
∴CN=BF,
∵∠CAD=∠BCG=22.5°,
∵AC=BC,
∴△ACN≌△CBF,
∴CF=AN=2CE,
∴AD=DE+EN+AN=2DE+CF=2DE+2CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
 的图象的对称轴是直线
的图象的对称轴是直线 ,其图象的一部分如图所示则:①
,其图象的一部分如图所示则:① ;②
;② ;③
;③ ;④
;④ ;⑤当
;⑤当 时,
时, .其中判断正确的有( )个.
.其中判断正确的有( )个.
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示为二次函数
 的图象,在下列选项中错误的是( )
的图象,在下列选项中错误的是( )
A.

B.
 时,
时, 随
随 的增大而增大
的增大而增大C.

D. 方程
 的根是
的根是 ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系xOy中的线段AB及点P,给出如下定义:
若点P满足PA=PB,则称P为线段AB的“轴点”,其中,当0°<∠APB<60°时,称P为线段AB的“远轴点”;当60°≤∠APB≤180°时,称P为线段AB的“近轴点”.
(1)如图1,点A,B的坐标分别为(-2,0),(2,0),则在
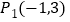 ,
, ,
, ,
, 中,线段AB的“近轴点”是 .
中,线段AB的“近轴点”是 .(2)如图2,点A的坐标为(3,0),点B在y轴正半轴上,且∠OAB=30°.
①若P为线段AB的“远轴点”,直接写出点P的横坐标t的取值范围 ;
②点C为y轴上的动点(不与点B重合且BC≠AB),若Q为线段AB的“轴点”,当线段QB与QC的和最小时,求点Q的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
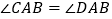 ,则在下列条件:①∠C=∠D ②AC=AD ③∠CBA=∠DBA ④BC=BD中任选一个能判定△ABC≌△ABD的是( )
,则在下列条件:①∠C=∠D ②AC=AD ③∠CBA=∠DBA ④BC=BD中任选一个能判定△ABC≌△ABD的是( )
A. ①②③④ B. ②③④ C. ①③④ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=900,AC=BC,AE平分∠BAC与BC交于点E, DE⊥AB于点D,若AB=8cm,则△DEB的周长为( )

A.4cmB.6cmC.8cmD.10cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BD⊥AC,CE⊥AB,垂足分别为D、E,BD、CE交于点O,且AO平分∠BAC,,那么图中全等三角形有_________对.

相关试题

