【题目】已知二次函数图象的顶点坐标为(0,1),且过点(﹣1, ![]() ),直线y=kx+2与y轴相交于点P,与二次函数图象交于不同的两点A(x1 , y1),B(x2 , y2). (注:在解题过程中,你也可以阅读后面的材料)
),直线y=kx+2与y轴相交于点P,与二次函数图象交于不同的两点A(x1 , y1),B(x2 , y2). (注:在解题过程中,你也可以阅读后面的材料)
附:阅读材料
任何一个一元二次方程的根与系数的关系为:两根的和等于一次项系数与二次项系数的比的相反数,两根的积等于常数项与二次项系数的比.
即:设一元二次方程ax2+bx+c=0的两根为x1 , x2 ,
则:x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]()
能灵活运用这种关系,有时可以使解题更为简单.
例:不解方程,求方程x2﹣3x=15两根的和与积.
解:原方程变为:x2﹣3x﹣15=0
∵一元二次方程的根与系数有关系:x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]()
∴原方程两根之和=﹣ ![]() =3,两根之积=
=3,两根之积= ![]() =﹣15.
=﹣15.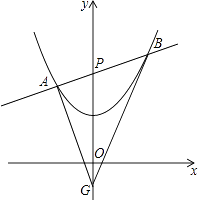
(1)求该二次函数的解析式.
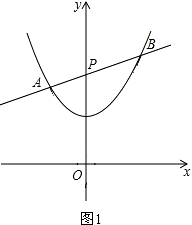
(2)对(1)中的二次函数,当自变量x取值范围在﹣1<x<3时,请写出其函数值y的取值范围;(不必说明理由)
(3)求证:在此二次函数图象下方的y轴上,必存在定点G,使△ABG的内切圆的圆心落在y轴上,并求△GAB面积的最小值.
参考答案:
【答案】
(1)解:由于二次函数图象的顶点坐标为(0,1),
因此二次函数的解析式可设为y=ax2+1.
∵抛物线y=ax2+1过点(﹣1, ![]() ),
),
∴ ![]() =a+1.
=a+1.
解得:a= ![]() .
.
∴二次函数的解析式为:y= ![]() x2+1
x2+1
(2)解:当x=﹣1时,y= ![]() ,
,
当x=0时,y=1,
当x=3时,y= ![]() ×32+1=
×32+1= ![]() ,
,
结合图1可得:当﹣1<x<3时,y的取值范围是1≤y< ![]()
(3)①证明:过点A作y轴的对称点A′,连接BA′并延长,交y轴于点G,连接AG,如图2,
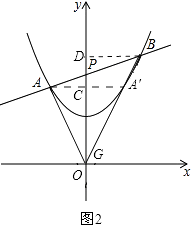
则点A′必在抛物线上,且∠AGP=∠BGP,
∴△ABG的内切圆的圆心落在y轴上.
∵点A的坐标为(x1,y1),
∴点A′的坐标为(﹣x1,y1).
∵点A(x1,y1)、B(x2,y2)在直线y=kx+2上,
∴y1=kx1+2,y2=kx2+2.
∴点A′的坐标为(﹣x1,kx1+2)、点B的坐标为(x2,kx2+2).
设直线BG的解析式为y=mx+n,则点G的坐标为(0,n).
∵点A′(﹣x1,kx1+2)、B(x2,kx2+2)在直线BG上,
∴ ![]() .
.
解得: 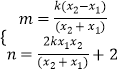 .
.
∵A(x1,y1),B(x2,y2)是直线y=kx+2与抛物线y= ![]() x2+1的交点,
x2+1的交点,
∴x1、x2是方程kx+2= ![]() x2+1即x2﹣4kx﹣4=0的两个实数根.
x2+1即x2﹣4kx﹣4=0的两个实数根.
∴由根与系数的关系可得;x1+x2=4k,x1x2=﹣4.
∴n= ![]() =﹣2+2=0.
=﹣2+2=0.
∴点G的坐标为(0,0).
∴在此二次函数图象下方的y轴上,存在定点G(0,0),使△ABG的内切圆的圆心落在y轴上.
②解:过点A作AC⊥OP,垂足为C,过点B作BD⊥OP,垂足为D,如图2,

∵直线y=kx+2与y轴相交于点P,
∴点P的坐标为(0,2).
∴PG=2.
∴S△ABG=S△APG+S△BPG
= ![]() PGAC+
PGAC+ ![]() PGBD
PGBD
= ![]() PG(AC+BD)
PG(AC+BD)
= ![]() ×2×(﹣x1+x2)
×2×(﹣x1+x2)
=x2﹣x1
= ![]()
= ![]()
= ![]()
=4 ![]() .
.
∴当k=0时,S△ABG最小,最小值为4.
∴△GAB面积的最小值为4.
【解析】(1)设二次函数解析式为y=ax2+1,由于点(﹣1, ![]() )在二次函数图象上,把该点的坐标代入y=ax2+1,即可求出a,从而求出二次函数的解析式.(2)先分别求出x=﹣1,x=0,x=3时y的值,然后结合图象就可得到y的取值范围.(3)过点A作y轴的对称点A′,连接BA′并延长,交y轴于点G,连接AG,如图2,则点A′必在抛物线上,且∠AGP=∠BGP,由此可得△ABG的内切圆的圆心落在y轴上.由于点A(x1 , y1)、B(x2 , y2)在直线y=kx+2上,从而可以得到点A的坐标为(x1 , kx1+2)、A′的坐标为(﹣x1 , kx1+2)、B的坐标为(x2 , kx2+2).设直线BG的解析式为y=mx+n,则点G的坐标为(0,n).由于点A′(﹣x1 , kx1+2)、B(x2 , kx2+2)在直线BG上,可用含有k、x1、x2的代数式表示n.由于A、B是直线y=kx+2与抛物线y=
)在二次函数图象上,把该点的坐标代入y=ax2+1,即可求出a,从而求出二次函数的解析式.(2)先分别求出x=﹣1,x=0,x=3时y的值,然后结合图象就可得到y的取值范围.(3)过点A作y轴的对称点A′,连接BA′并延长,交y轴于点G,连接AG,如图2,则点A′必在抛物线上,且∠AGP=∠BGP,由此可得△ABG的内切圆的圆心落在y轴上.由于点A(x1 , y1)、B(x2 , y2)在直线y=kx+2上,从而可以得到点A的坐标为(x1 , kx1+2)、A′的坐标为(﹣x1 , kx1+2)、B的坐标为(x2 , kx2+2).设直线BG的解析式为y=mx+n,则点G的坐标为(0,n).由于点A′(﹣x1 , kx1+2)、B(x2 , kx2+2)在直线BG上,可用含有k、x1、x2的代数式表示n.由于A、B是直线y=kx+2与抛物线y= ![]() x2+1的交点,由根与系数的关系可得:x1+x2=4k,x1x2=﹣4.从而求出n=0,即可证出:在此二次函数图象下方的y轴上,存在定点G(0,0),使△ABG的内切圆的圆心落在y轴上.由S△ABG=S△APG+S△BPG , 可以得到S△ABG=x2﹣x1=
x2+1的交点,由根与系数的关系可得:x1+x2=4k,x1x2=﹣4.从而求出n=0,即可证出:在此二次函数图象下方的y轴上,存在定点G(0,0),使△ABG的内切圆的圆心落在y轴上.由S△ABG=S△APG+S△BPG , 可以得到S△ABG=x2﹣x1= ![]() =4
=4 ![]() ,所以当k=0时,S△ABG最小,最小值为4.
,所以当k=0时,S△ABG最小,最小值为4.
【考点精析】认真审题,首先需要了解根与系数的关系(一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商),还要掌握确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC的角平分线AD交BC于E,交△ABC的外接圆⊙O于D.
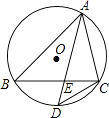
(1)求证:△ABE∽△ADC;
(2)请连接BD,OB,OC,OD,且OD交BC于点F,若点F恰好是OD的中点.求证:四边形OBDC是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店周年庆,印刷了1000张奖券,其中印有老虎图案的有10张,每张奖金1000元,印有羊图案的有50张,每张奖金100元,印有鸡图案的有100张,每张奖金20元,印有兔子图案的有400张,每张奖金2元,其余印有花朵图案但无奖金,从中任意抽取一张,请解答下列问题:
(1)获得1000元奖金的概率是多少?
(2)获得奖金的概率是多少?
(3)若要使获得2元奖金的概率为
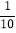 ,则需要将多少张印有花朵图案的奖券换为印有兔子图案的奖券?
,则需要将多少张印有花朵图案的奖券换为印有兔子图案的奖券? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q.
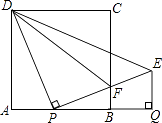
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数;
(2)如图2,AB∥CD,AB=CD,BF=DE,求证:∠AEF=∠CFB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设一列数
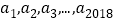 中任意三个相邻的数之和都是22,已知
中任意三个相邻的数之和都是22,已知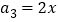 ,
,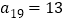 ,
, ,那么
,那么 =________.
=________. -
科目: 来源: 题型:
查看答案和解析>>【题目】火车站、机场、邮局等场所都有为旅客提供打包服务的项目.现有一个长、宽、高分别为a、b 、30的箱子(其中a>b),准备采用如图①、②的两种打包方式,所用打包带的总长(不计接头处的长)分别记为
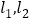 .
. 
(1)图①中打包带的总长
 =________.
=________. 图②中打包带的总长
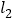 =________.
=________.(2)试判断哪一种打包方式更节省材料,并说明理由.(提醒:先判断再说理,说理过程即为比较
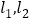 的大小.)
的大小.) (3)若b=40且a为正整数,在数轴上表示数
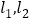 的两点之间有且只有19个整数点,求a 的值.
的两点之间有且只有19个整数点,求a 的值.
相关试题

