搜索
【题目】设一列数
中任意三个相邻的数之和都是22，已知
，
，
，那么
=________．
参考答案：
【答案】5
【解析】
由任意三个相邻数之和都是22，可知a1、a4、a7、…a3n+1相等，a2、a5、a8、…a3n+2相等，a3、a6、a9、…a3n相等，可以得出a19=a1=13，a66=a3=2x，根据
可求出x的值,再根据任意三个相邻的数之和都是22,可求出相邻的三个数的值,问题得以解决．
解：由任意三个相邻数之和都是22可知：
a1+a2+a3=22，
a2+a3+a4=22，
a3+a4+a5=22，
…
an+an+1+an+2=22，
可以推出：a1=a4=a7=…=a3n+1，
a2=a5=a8=…=a3n+2，
a3=a6=a9=…=a3n，
所以a19=a1=13，a66=a3，
则2x=6-x，
解得x=2，
所以a2=22-4-13=5，
因此a2018=a2=5．
故答案为：5.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的边长为1，AB边上有一动点P，连接PD，线段PD绕点P顺时针旋转90°后，得到线段PE，且PE交BC于F，连接DF，过点E作EQ⊥AB的延长线于点Q．
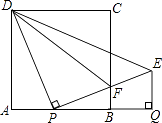
（1）求线段PQ的长；
（2）问：点P在何处时，△PFD∽△BFP，并说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数图象的顶点坐标为（0，1），且过点（﹣1，
），直线y=kx+2与y轴相交于点P，与二次函数图象交于不同的两点A（x1 ， y1），B（x2 ， y2）． （注：在解题过程中，你也可以阅读后面的材料）
附：阅读材料
任何一个一元二次方程的根与系数的关系为：两根的和等于一次项系数与二次项系数的比的相反数，两根的积等于常数项与二次项系数的比．
即：设一元二次方程ax2+bx+c=0的两根为x1 ， x2 ，
则：x1+x2=﹣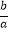
，x1x2=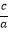 
能灵活运用这种关系，有时可以使解题更为简单．
例：不解方程，求方程x2﹣3x=15两根的和与积．
解：原方程变为：x2﹣3x﹣15=0
∵一元二次方程的根与系数有关系：x1+x2=﹣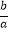 ，x1x2=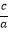
∴原方程两根之和=﹣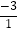
=3，两根之积= 
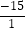=﹣15．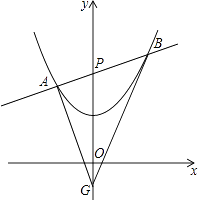
（1）求该二次函数的解析式．
（2）对（1）中的二次函数，当自变量x取值范围在﹣1＜x＜3时，请写出其函数值y的取值范围；（不必说明理由）
（3）求证：在此二次函数图象下方的y轴上，必存在定点G，使△ABG的内切圆的圆心落在y轴上，并求△GAB面积的最小值． -
科目： 来源： 题型：
查看答案和解析>>【题目】(1)如图1,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数；
(2)如图2,AB∥CD,AB=CD,BF=DE,求证:∠AEF=∠CFB.
-
科目： 来源： 题型：
查看答案和解析>>【题目】火车站、机场、邮局等场所都有为旅客提供打包服务的项目．现有一个长、宽、高分别为a、b 、30的箱子（其中a＞b），准备采用如图①、②的两种打包方式，所用打包带的总长（不计接头处的长）分别记为
． 
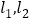（1）图①中打包带的总长
=________． 图②中打包带的总长
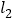=________．（2）试判断哪一种打包方式更节省材料，并说明理由．（提醒：先判断再说理，说理过程即为比较
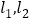的大小．） （3）若b=40且a为正整数，在数轴上表示数
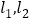的两点之间有且只有19个整数点，求a 的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知A＝x－2y，B＝－x－4y＋1.
（1）求2(A＋B)－(A－B)；（结果用含x，y的代数式表示）
（2）当
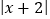与
互为相反数时，求(1)中代数式的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】一位射击运动员在10次射击训练中，命中靶的环数如图． 请你根据图表，完成下列问题：
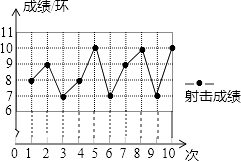
（1）补充完成下面成绩表单的填写：射击序次
1
2
3
4
5
6
7
8
9
10
成绩/环
8
10
7
9
10
7
10
（2）求该运动员这10次射击训练的平均成绩．
相关试题
