【题目】汽车租赁行业现在火爆起来.小明开办了一家汽车租赁公司,拥有汽车20辆,在旺季每辆车的每天租金为600元时,可全部租出:当每辆车的每天租金增加50元时,未租出的车将增加一辆,租出的车辆每辆每天需要维护费200元,未租出的车辆每辆每天需要维护费100元,每天其他开销共计1000元.
(1)当每辆车的租金为1000元时,每天能租出多少辆车?每天净收益为多少元?
(2)当每辆车的每天租金定为多少元时,租赁公司的每天净收益最大?最大净收益为多少元?(每天净收益=总租金﹣租出去车辆维护费﹣未租出去车辆维护费﹣每天其他开销)
参考答案:
【答案】(1)当每辆车的租金为1000元时,每天能租出12辆车,每天净收益为7800元;(2)当每辆车的每天租金定为850元时,租赁公司的每天净收益最大,最大净收益为8250元.
【解析】
(1)根据:租出的车=20﹣![]() , 每天净收益=总租金﹣租出去车辆维护费﹣未租出去车辆维护费﹣每天其他开销,列式计算可得;
, 每天净收益=总租金﹣租出去车辆维护费﹣未租出去车辆维护费﹣每天其他开销,列式计算可得;
(2)根据:每天净收益=总租金﹣租出去车辆维护费﹣未租出去车辆维护费﹣每天其他开销列出函数关系式,根据二次函数性质可得最值情况.
(1)当每辆车的租金为x元时,每天租出的车有:20﹣ ![]() =12(辆),每天的净收益为:12×(1000﹣200)﹣8×100﹣1000=7800元,答:当每辆车的租金为1000元时,每天能租出12辆车,每天净收益为7800元.
=12(辆),每天的净收益为:12×(1000﹣200)﹣8×100﹣1000=7800元,答:当每辆车的租金为1000元时,每天能租出12辆车,每天净收益为7800元.
(2)设每辆车每天的租金为x元,每天的净收益为y元,根据题意,得:y=(x﹣200)(20﹣ ![]() )﹣
)﹣![]() ×100﹣1000
×100﹣1000
=﹣![]() x2+34x﹣6200.
x2+34x﹣6200.
∵a=﹣![]() <0,∴当x=﹣
<0,∴当x=﹣ ![]() =850元时,y取得最大值8250元,答:当每辆车的每天租金定为850元时,租赁公司的每天净收益最大,最大净收益为8250元.
=850元时,y取得最大值8250元,答:当每辆车的每天租金定为850元时,租赁公司的每天净收益最大,最大净收益为8250元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数
 (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA= .
.(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠C=90,AC=4cm,BC=3cm,点P由点B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由点A出发沿AC方向向点C匀速运动,速度为2cm/s;连结PQ。若设运动时间为t(s)(0<t<2),解答下列问题:

(1)当t为何值时?PQ//BC?
(2)设△APQ的面积为y(cm2),求y与t之间的函数关系?
(3)是否存在某一时刻t,使线段PQ恰好把△ABC的周长和面积同时平分?若存在求出此时t的值;若不存在,说明理由。
(4)如图2,连结PC,并把△PQC沿AC翻折,得到四边形PQP'C,那么是否存在某一时刻t,使四边形PQP'C为菱形?若存在求出此时t的值;若不存在,说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
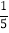 x﹣1与坐标轴交于A,B两点,点P是曲线y=
x﹣1与坐标轴交于A,B两点,点P是曲线y=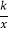 (x>0)上一点,若△PAB是以∠APB=90°的等腰三角形,则k= _________.
(x>0)上一点,若△PAB是以∠APB=90°的等腰三角形,则k= _________.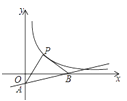
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2014年巴西世界杯足球赛前夕,某体育用品店购进一批单价为40元的球服,如果按单价60元销售,那么一个月内可售出240套,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套,设销售单价为x(120>x≥60)元,销售量为y套.
(1)求出y与x的函数关系式;
(2)当销售单价为多少元时,月销售额为14000元,此月共盈利多少元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.
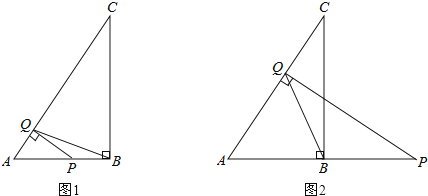
(1)当点P在线段AB上时,求证:△APQ∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.

相关试题

