Question

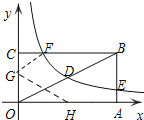
【题目】如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，点E（4，n）在边AB上，反比例函数（k≠0）在第一象限内的图象经过点D、E，且tan∠BOA=．

（1）求边AB的长；

（2）求反比例函数的解析式和n的值；

（3）若反比例函数的图象与矩形的边BC交于点F，将矩形折叠，使点O与点F重合，折痕分别与x、y轴正半轴交于点H、G，求线段OG的长．

Answer 1

【答案】（1）2

y=，n=；

OG=．

【解析】（1）∵点E（4，n）在边AB上，

∴OA=4，

在Rt△AOB中，∵tan∠BOA=，

∴AB=OA×tan∠BOA=4×=2；

（2）根据（1），可得点B的坐标为（4，2），

∵点D为OB的中点，

∴点D（2，1）

∴=1，

解得k=2，

∴反比例函数解析式为y=，

又∵点E（4，n）在反比例函数图象上，

∴=n，

解得n=；

（3）如图，设点F（a，2），

∵反比例函数的图象与矩形的边BC交于点F，

∴=2，

解得a=1，

∴CF=1，

连接FG，设OG=t，则OG=FG=t，CG=2﹣t，

在Rt△CGF中，GF2=CF2+CG2，

即t2=（2﹣t）2+12，

解得t=，

∴OG=t=．