【题目】已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.
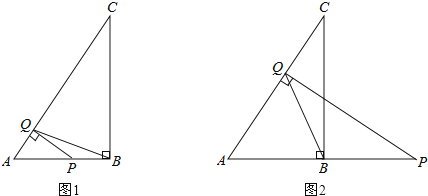
(1)当点P在线段AB上时,求证:△APQ∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
参考答案:
【答案】解:(1)证明:∵∠A+∠APQ=90°,∠A+∠C=90°,∴∠APQ=∠C。
在△APQ与△ABC中,∵∠APQ=∠C,∠A=∠A,
∴△APQ∽△ABC。
(2)在Rt△ABC中,AB=3,BC=4,由勾股定理得:AC=5。
∵∠BPQ为钝角,∴当△PQB为等腰三角形时,只可能是PB=PQ。
(I)当点P在线段AB上时,如题图1所示,
由(1)可知,△APQ∽△ABC,
∴![]() ,即
,即![]() ,解得:
,解得:![]() 。
。
∴![]() 。
。
(II)当点P在线段AB的延长线上时,如题图2所示,
∵BP=BQ,∴∠BQP=∠P。
∵∠BQP+∠AQB=90°,∠A+∠P=90°,∴∠AQB=∠A。∴BQ=AB。
∴AB=BP,点B为线段AB中点。
∴AP=2AB=2×3=6。
综上所述,当△PQB为等腰三角形时,AP的长为![]() 或6。
或6。
【解析】
试题(1)由两对角相等(∠APQ=∠C,∠A=∠A),证明△APQ∽△ABC。
(2)当△PQB为等腰三角形时,有两种情况,需要分类讨论.
(I)当点P在线段AB上时,如题图1所示.由三角形相似(△APQ∽△ABC)关系计算AP的长;
(II)当点P在线段AB的延长线上时,如题图2所示.利用角之间的关系,证明点B为线段AP的中点,从而可以求出AP。
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的例题,再按要求解答后面的问题.
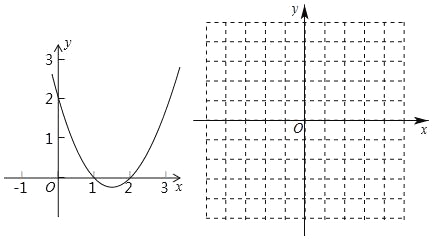
例题:解一元二次不等式x2﹣3x+2>0
解:令y=x2﹣3x+2,画出y=x2﹣3x+2如图所示,由图象可知:
当x<1或x>2时,y>0所以一元二次不等式x2﹣3x+2>0的解集为x<1或x>2
(1)填空:x2﹣3x+2<0的解集为 ;x2﹣3x≥0的解集为 .
(2)用类似的方法解一元二次不等式:﹣x2﹣2x+3>0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】山地自行车越来越受中学生的喜爱.一网店经营的一个型号山地自行车,今年一月份销售额为30000元,二月份每辆车售价比一月份每辆车售价降价100元,若销售的数量与上一月销售的数量相同,则销售额是27000元.
(1)求二月份每辆车售价是多少元?
(2)为了促销,三月份每辆车售价比二月份每辆车售价降低了10%销售,网店仍可获利35%,求每辆山地自行车的进价是多少元?
-
科目: 来源: 题型:
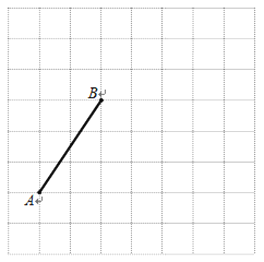
查看答案和解析>>【题目】下图是由边长为1个单位长度的小正方形组成的网格,线段AB的端点在格点上.
(1)请建立适当的平面直角坐标系xOy,使得A点的坐标为(-3,-1),在此坐标系下,B点的坐标为________________;
(2)将线段BA绕点B逆时针旋转90°得线段BC,画出BC;在第(1)题的坐标系下,C点的坐标为__________________;
(3)在第(1)题的坐标系下,二次函数y=ax2+bx+c(a≠0)的图象过O、B、C三点,则此函数图象的对称轴方程是________________.
【答案】 (-1,2) (2,0) x=1
【解析】分析:
 根据点
根据点 的坐标建立坐标系,即可写出点
的坐标建立坐标系,即可写出点 的坐标.
的坐标. 画出点
画出点 旋转后的对应点
旋转后的对应点 连接
连接 ,写出点
,写出点 的坐标.
的坐标. 用待定系数法求出函数解析式,即可求出对称轴方程.
用待定系数法求出函数解析式,即可求出对称轴方程.详解:(1)建立坐标系如图,
B点的坐标为
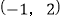 ;
;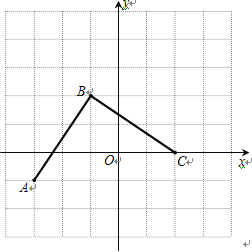
(2)线段BC如图,C点的坐标为
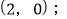
(3)把点
 代入二次函数
代入二次函数 ,得
,得
解得:

二次函数解析为:
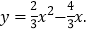
对称轴方程为:
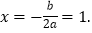
故对称轴方程是

点睛:考查图形与坐标;旋转、对称变换;待定系数法求二次函数解析式,二次函数的图象与性质.熟练掌握各个知识点是解题的关键.
【题型】解答题
【结束】
18【题目】特殊两位数乘法的速算——如果两个两位数的十位数字相同,个位数字相加为10,那么能立说出这两个两位数的乘积.如果这两个两位数分别写作AB和AC(即十位数字为A,个位数字分别为B、C,B+C=10,A>3),那么它们的乘积是一个4位数,前两位数字是A和(A+1)的乘积,后两位数字就是B和C的乘积.
如:47×43=2021,61×69=4209.
(1)请你直接写出83×87的值;
(2)设这两个两位数的十位数字为x(
x>3),个位数字分别为y和z(y+z=10),通过计算验证这两个两位数的乘积为100x(x+1)+yz. (3)99991×99999=___________________(直接填结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=
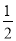 x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).(1)求二次函数的解析式.
(2)求函数图象的顶点坐标及D点的坐标.
(3)该二次函数的对称轴交x轴于C点.连接BC,并延长BC交抛物线于E点,连接BD,DE,求△BDE的面积.
(4)抛物线上有一个动点P,与A,D两点构成△ADP,是否存在S△ADP=
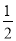 S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.
S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.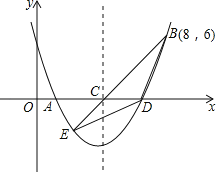
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.若四边形ABCD的面积记为S1,中点四边形EFGH的面积记为S2,则S1与S2的数量关系是( )
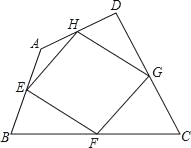
A. S1=3S2 B. 2S1=3S2 C. S1=2S2 D. 3S1=4S2
相关试题

