【题目】如图,四边形ABCD中,AB//CD,AD//BC,E,F是对角线BD上的两点,如果添加一个条件使![]() ,则添加的条件不能是( )
,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
参考答案:
【答案】A
【解析】
根据“平行四边形的判定和性质”结合“全等三角形的判定方法”进行分析判断即可.
∵AB//CD,AD//BC,
∴∠ABE=∠CDF,四边形ABCD是平行四边形,
∴AB=CD,
即在△ABE和△CDF中,已经有∠ABE=∠CDF和AB=CD两个条件,
∴(1)当添加条件AE=CF时,在△ABE和△CDF中有两边和其中一边的对角对应相等,此时不能判定两三角形全等,故可以选A;
(2)当添加条件BE=FD时,在△ABE和△CDF中有两边及其夹角对应相等,此时能够判断两三角形全等,故不能选B;
(3)当添加条件BF=DE时,由等式的性质可证得BE=FD,由(2)可知此时△ABE和△CDF全等,故不能选C;
(4)当添加条件∠1=∠2时,在△ABE和△CDF中有两角及其夹边对应相等,此时能判断两个三角形全等,故不能选D.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)
 ;(2)
;(2) .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生课余活动情况,某校对参加绘画、书法、舞蹈、乐器这四个课外兴趣小组的人员分布情况进行抽样调查,并根据收集的数据绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下面的问题:

(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中书法部分的圆心角的度数;
(3)如果该校共有1000名学生参加这4个课外兴趣小组,而每个教师最多只能辅导本组的20名学生,估计每个兴趣小组至少需要准备多少名教师?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
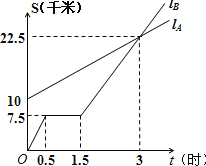
(1)B出发时与A相距 千米.
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是 小时.
(3)B出发后 小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于概率的叙述正确的是( )
A.某运动员投篮5次,投中4次,投中的概率为0.8
B.任意抛掷一枚硬币两次,结果是两个都是正面的概率是
C.数学选择题,四个选择支中有且只有一个正确,如果从中任选一个,选对的概率为
D.飞机失事死亡的概率为0.000000000038,因此乘飞机失事而死亡是不可能事件 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c)
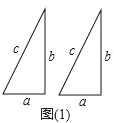
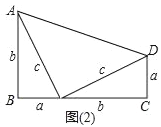
(1)用这样的两个三角形构造成如图(2)的图形,利用这个图形,证明:a2+b2=c2;
(2)用这样的两个三角形可以拼出多种四边形,画出周长最大的四边形;当a=2,b=4时,求这个四边形的周长;
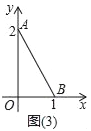
(3)当a=1,b=2时,将其中一个直角三角形放入平面直角坐标系中(如图(3)),使直角顶点与原点重合,两直角边a,b分别与x轴、y轴重合.
①请在x轴、y轴上找一点C,使△ABC为等腰三角形;(要求:用尺规画出所有符合条件的点,并用C1,C2,…,Cn在图中标出所找的点.只保留作图痕迹,不写作法)
②写出一个满足条件的在x轴上的点的坐标:_____,写出一个满足条件的在y轴上的点坐标:_____.
相关试题

