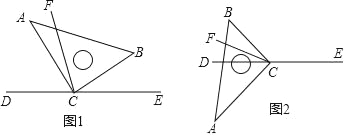
【题目】直角三角板ABC的直角顶点C在直线DE上,CF平分∠BCD.
(1)在图1中,若∠BCE=40°,求∠ACF的度数;
(2)在图1中,若∠BCE=α,直接写出∠ACF的度数(用含α的式子表示);
(3)将图1中的三角板ABC绕顶点C旋转至图2的位置,探究:写出∠ACF与∠BCE的度数之间的关系,并说明理由.
参考答案:
【答案】(1)∠ACF=20°;(2)∠ACF=![]() α;(3)∠ACF=
α;(3)∠ACF=![]() ∠BCE.理由见解析.
∠BCE.理由见解析.
【解析】试题分析:(1)由∠ACB=90°,∠BCE=40°,可得∠ACD,∠BCD的度数,再根据CF平分∠BCD,可得∠DCF的度数,继而可求得∠ACF=∠DCF﹣∠ACD=20°;
(2)由∠ACB=90°,∠BCE=α°,可得∠ACD=90°﹣α,∠BCD=180°﹣α,再根据CF平分∠BCD,从而可得∠DCF=90°﹣![]() α,继而可得∠ACF=
α,继而可得∠ACF=![]() α;
α;
(3)由点C在DE上,可得∠BCD=180°﹣∠BCE,再根据CF平分∠BCD,可得∠BCF=90°-![]() ∠BCE,再根据∠ACB=90°,从而有∠ACF=
∠BCE,再根据∠ACB=90°,从而有∠ACF=![]() ∠BCE.
∠BCE.
试题解析:(1)如图1,∵∠ACB=90°,∠BCE=40°,
∴∠ACD=180°﹣90°﹣40°=50°,∠BCD=180°﹣40°=140°,
又CF平分∠BCD,
∴∠DCF=∠BCF=![]() ∠BCD=70°,
∠BCD=70°,
∴∠ACF=∠DCF﹣∠ACD=70°﹣50°=20°;
(2)如图1,∵∠ACB=90°,∠BCE=α°,
∴∠ACD=180°﹣90°﹣α°=90°﹣α,∠BCD=180°﹣α,
又CF平分∠BCD,
∴∠DCF=∠BCF=![]() ∠BCD=90°﹣
∠BCD=90°﹣![]() α,
α,
∴∠ACF=90°﹣![]() α﹣90°+α=
α﹣90°+α=![]() α;
α;
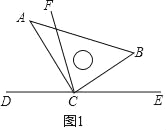
(3)∠ACF=![]() ∠BCE.理由如下:
∠BCE.理由如下:
如图2,∵点C在DE上,
∴∠BCD=180°﹣∠BCE.
∵CF平分∠BCD,
∴∠BCF=![]() ∠BCD=
∠BCD=![]() (180°﹣∠BCE)=90°-
(180°﹣∠BCE)=90°-![]() ∠BCE.
∠BCE.
∵∠ACB=90°,
∴∠ACF=∠ACB﹣∠BCF=90°﹣(90°-![]() ∠BCE)=
∠BCE)=![]() ∠BCE.
∠BCE.
即:∠ACF=![]() ∠BCE.
∠BCE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲乙两厂的印刷费用y(千元)与证书数量x(千个)的函数关系图象分别如图中甲、乙所示.

(1)填空:甲厂的制版费是________千元,当x≤2(千个)时乙厂证书印刷单价是________元/个;
(2)求出甲厂的印刷费y甲与证书数量x的函数关系式,并求出其证书印刷单价;
(3)当印制证书8千个时,应选择哪个印刷厂节省费用,节省费用多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=﹣3是关于x的方程(k+3)x+2=3x﹣2k的解.
(1)求k的值;
(2)在(1)的条件下,已知线段AB=6cm,点C是直线AB上一点,且BC=kAC,若点D是AC的中点,求线段CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求出符合条件的二次函数解析式:
(1)二次函数图象经过点(﹣1,0),(1,2),(0,3);
(2)二次函数图象的顶点坐标为(﹣3,6),且经过点(﹣2,10);
(3)二次函数图象与x轴的交点坐标为(﹣1,0),(3,0),与y轴交点的纵坐标为9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新学期开学,某体育用品商店开展促销活动,有两种优惠方案.
方案一:不购买会员卡时,乒乓球享受8.5折优惠,乒乓球拍购买5副(含5副)以上才能享受8.5折优惠,5副以下必须按标价购买.
方案二:办理会员卡时,全部商品享受八折优惠,小健和小康的谈话内容如下:

会员卡只限本人使用.
(1)求该商店销售的乒乓球拍每副的标价.
(2)如果乒乓球每盒10元,小健需购买乒乓球拍6副,乒乓球a盒,请回答下列问题:
①如果方案一与方案二所付钱数一样多,求a的值;
②直接写出一个恰当的a值,使方案一比方案二优惠;
③直接写出一个恰当的a值,使方案二比方案一优惠.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣1,0)、B(2,0)两点,交y轴于点C(0,﹣2),过点A、C画直线.
(1)求二次函数的解析式;
(2)若点P在x轴正半轴上,且PA=PC,求OP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在直角三角形ABC中,∠ACB=900,D是AB上一点,且∠ACD=∠B
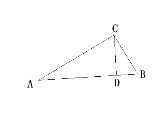
(1)判断△ACD的形状?并说明理由。
(2)你在证明你的结论过程中应用了哪一对互逆的真命题?
相关试题

