【题目】已知,如图,在直角三角形ABC中,∠ACB=900,D是AB上一点,且∠ACD=∠B
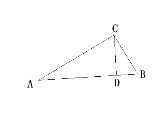
(1)判断△ACD的形状?并说明理由。
(2)你在证明你的结论过程中应用了哪一对互逆的真命题?
参考答案:
【答案】答:△ACD是直角三角形 理由:可证△ACD∽△ABC ,对应角∠ACD=∠ACB=90°所以CD⊥AB
互逆的真命题:两个三角形相似,对应角相等。
两个直角三角形对应角相等,则两个三角形相似。
【解析】
试题分析:依题意知∠ACD=∠B,且∠A =∠A,可得△ACD∽△ABC。因为∠ACB=900
所以对应角∠ACD=∠ACB=90°。则△ACD是直角三角形
(2)互逆的真命题:两个三角形相似,对应角相等。
两个直角三角形对应角相等,则两个三角形相似。
-
科目: 来源: 题型:
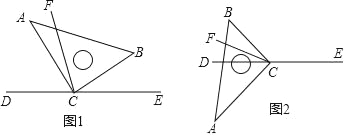
查看答案和解析>>【题目】直角三角板ABC的直角顶点C在直线DE上,CF平分∠BCD.
(1)在图1中,若∠BCE=40°,求∠ACF的度数;
(2)在图1中,若∠BCE=α,直接写出∠ACF的度数(用含α的式子表示);
(3)将图1中的三角板ABC绕顶点C旋转至图2的位置,探究:写出∠ACF与∠BCE的度数之间的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新学期开学,某体育用品商店开展促销活动,有两种优惠方案.
方案一:不购买会员卡时,乒乓球享受8.5折优惠,乒乓球拍购买5副(含5副)以上才能享受8.5折优惠,5副以下必须按标价购买.
方案二:办理会员卡时,全部商品享受八折优惠,小健和小康的谈话内容如下:

会员卡只限本人使用.
(1)求该商店销售的乒乓球拍每副的标价.
(2)如果乒乓球每盒10元,小健需购买乒乓球拍6副,乒乓球a盒,请回答下列问题:
①如果方案一与方案二所付钱数一样多,求a的值;
②直接写出一个恰当的a值,使方案一比方案二优惠;
③直接写出一个恰当的a值,使方案二比方案一优惠.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣1,0)、B(2,0)两点,交y轴于点C(0,﹣2),过点A、C画直线.
(1)求二次函数的解析式;
(2)若点P在x轴正半轴上,且PA=PC,求OP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 (m>0)与x轴交于A、B两点.
(m>0)与x轴交于A、B两点.(1)求证:抛物线的对称轴在y轴的左侧;
(2)若
 (O为坐标原点),求抛物线的解析式;
(O为坐标原点),求抛物线的解析式;(3)设抛物线与y轴交于点C,若△ABC是直角三角形.求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.

(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD∥CB,∠A=∠C,若∠ABD=32°,求∠BDC的度数.有同学用了下面的方法.但由于一时犯急没有写完整,请你帮他添写完整.
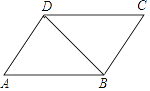
解:∵AD∥CB(已知)
∴∠C+∠ADC=180°(_________________),
又∵∠A=∠C (___________________),
∴∠A+∠ADC=180° (___________________),
∴AB∥CD (___________________________),
∴∠BDC=∠ABD=32° (___________________).
相关试题

