搜索
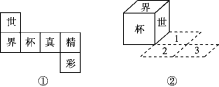
【题目】如图①所示的是一个正方体的表面展开图，将对应的正方体从如图②所示的位置依次翻到第1格、第2格、第3格，这时正方体朝上的一面上的字是________．
参考答案：
【答案】真
【解析】
注意正方体的空间图形,从相对面入手,分析及解答问题.对于此类问题一般方法是用纸按图的样子折叠后可以解决,或是在对展开图理解的基础上直接想象.从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.正方体的展开图有11种情况,分析平面展开图的各种情况后再认真确定哪两个面的对面.
解:由图①可知,“界”和“真”相对,“杯”和“精”相对,“世”和“彩”相对，由图②可知,小正方体依次翻到第1格、第2格、第3格时,底面上的字是“界”,故朝上面的字是“真”.
故答案为：真.
-
科目： 来源： 题型：
查看答案和解析>>【题目】把长为20，宽为a的长方形纸片(10＜a＜20)，如图那样折一下，剪下一个边长等于长方形宽度的正方形(称为第一次操作)；再把剩下的长方形如图那样折一下，剪下一个边长等于此时长方形宽度的正方形(称为第二次操作)；如此反复操作下去，若在第n次操作后，剩下的长方形为正方形，则操作停止．当n=3时，a的值为________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点O为Rt△ABC斜边AB上一点，以OA为半径的⊙O与BC相切于点D，与AC相交于点E，与AB相交于点F，连接AD．
（1）求证：AD平分∠BAC；
（2）若点E为弧AD的中点，探究线段BD，CD之间的数量关系，并证明你的结论；
（3）若点E为弧AD的中点，CD=
，求弧DF与线段BD，BF所围成的阴影部分的面积．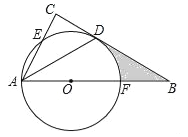
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠C=90°，以AC为直径作⊙O，交AB于D，过点O作OE∥AB，交BC于E．
（1）求证：ED为⊙O的切线；
（2）如果⊙O的半径为
，ED=2，延长EO交⊙O于F，连接DF、AF，求△ADF的面积．
【答案】（1）证明见解析；（2）
【解析】试题分析：（1）首先连接OD，由OE∥AB，根据平行线与等腰三角形的性质，易证得
≌
即可得
，则可证得
为
的切线；
（2）连接CD，根据直径所对的圆周角是直角，即可得
利用勾股定理即可求得
的长，又由OE∥AB，证得
根据相似三角形的对应边成比例，即可求得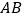
的长，然后利用三角函数的知识，求得
与
的长，然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案．试题解析：(1)证明：连接OD，
∵OE∥AB，
∴∠COE=∠CAD，∠EOD=∠ODA，
∵OA=OD,
∴∠OAD=∠ODA，
∴∠COE=∠DOE，
在△COE和△DOE中，
∴△COE≌△DOE(SAS)，
∴ED⊥OD，
∴ED是
的切线；(2)连接CD，交OE于M，
在Rt△ODE中，
∵OD=32，DE=2，
∵OE∥AB，
∴△COE∽△CAB，
∴AB=5，∵AC是直径，
∵EF∥AB，
∴S△ADF=S梯形ABEFS梯形DBEF
∴△ADF的面积为
【题型】解答题
【结束】
25【题目】【题目】已知，抛物线y=ax2+ax+b（a≠0）与直线y=2x+m有一个公共点M（1，0），且a＜b．
（1）求b与a的关系式和抛物线的顶点D坐标（用a的代数式表示）；
（2）直线与抛物线的另外一个交点记为N，求△DMN的面积与a的关系式；
（3）a=﹣1时，直线y=﹣2x与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移t个单位（t＞0），若线段GH与抛物线有两个不同的公共点，试求t的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系内，直线l⊥y轴于点C(C在y轴的正半轴上)，与直线y=
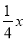相交于点A，和双曲线y=
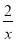交于点B，且AB=6，则点B的坐标是______． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线l经过⊙O的圆心O，且与⊙O交于A、B两点，点C在⊙O上，且∠AOC＝30°，点P是直线l上的一个动点(与圆心O不重合)，直线CP与⊙O相交于另一点Q，如果QP＝QO，则∠OCP＝ ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】张师傅在铺瓷砖时发现，用8块大小一样的小长方形瓷砖恰好可以拼成一个大的长方形，如图①．然后，他用这8块瓷砖又拼出一个正方形，如图②，中间恰好空出一个边长为1的小正方形（阴影部分）．
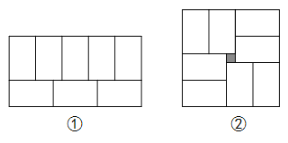
（1）请你根据图①写出小长方形的长与宽之比为 ；
（2）请你根据图②列出方程，求出小长方形的长与宽．
相关试题
