【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
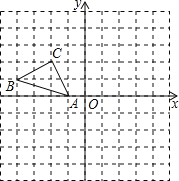
(1)作出△ABC绕点A逆时针旋转90°的△AB1C1,再作出△AB1C1关于原点O成中心对称的△A1B2C2.
(2)点B1的坐标为 ,点C2的坐标为 .
(3)△ABC经过怎样的旋转可得到△A1B2C2, .
参考答案:
【答案】(1)图解见解析(2)B1(﹣2,﹣3),C2(3,1);(3)△ABC绕点(0,﹣1)顺时针旋转90°
【解析】
试题分析:(1)根据网格结构找出点B、C的对应点B1、C1的位置,然后顺次连接即可,再找出点A1、B2、C2的位置,然后顺次连接即可;
(2)根据平面直角坐标系写出各点的坐标;
(3)根据图形,利用旋转的旋转解答.
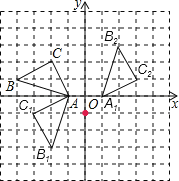
解:(1)△AB1C1,△A1B2C2如图所示;
(2)B1(﹣2,﹣3),C2(3,1);
(3)△ABC绕点(0,﹣1)顺时针旋转90°得到△A1B2C2.
故答案为:(2)(﹣2,﹣3),(3,1);(3)△ABC绕点(0,﹣1)顺时针旋转90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).

(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=2x2+3xy﹣2x﹣1,B=﹣x2+xy﹣1:
(1)求3A+6B;
(2)若3A+6B的值与x无关,求y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB上有两点C、D,且AC=BD,M、N分别是线段AC 、AD的中点,若AB=a cm ,AC=BD=b cm,且a,b满足(a-9)2+|b-7 |=0.

(1)求AB ,AC的长度;
(2)求线段MN的长度.
-
科目: 来源: 题型:
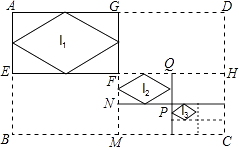
查看答案和解析>>【题目】如图,已知矩形ABCD的长和宽分别为16cm和12cm,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形l1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形l2;…如此操作下去,则l4的面积是cm2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB表示路灯,当身高为1.6米的小名站在离路灯1.6的D处时,他测得自己在路灯下的影长DE与身高CD相等,当小明继续沿直线BD往前走到E点时,画出此时小明的影子,并计算此时小明的影长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】两枚正四面体骰子的各面上分别标有数字1,2,3,4,现在同时投掷这两枚骰子,并分别记录着地的面所得的点数为a、b.
(1)假设两枚正四面体都是质地均匀,各面着地的可能性相同,请你在下面表格内列举出所有情形(例如(1,2),表示a=1,b=2),并求出两次着地的面点数相同的概率.b
a1
2
3
4
1
(1,2)
2
3
4
(2)为了验证试验用的正四面体质地是否均匀,小明和他的同学取一枚正四面体进行投掷试验.试验中标号为1的面着地的数据如下:试验总次数
50
100
150
200
250
500
“标号1”的面着地的次数
15
26
34
48
63
125
“标号1”的面着地的频率
0.3
0.26
0.23
0.24
请完成表格(数字精确到0.01),并根据表格中的数据估计“标号1的面着地”的概率是

相关试题

