搜索
【题目】如图△ABC是正三角形，曲线CDEF叫做“正三角形的渐开线”，其中 
、 
、 
圆心依次按A、B、C…循环，它们依次相连接．若AB=1，则曲线CDEF长是（结果保留π）． 
参考答案：
【答案】4π
【解析】解：弧CD的长是 
= 
，
弧DE的长是： 
= 
，
弧EF的长是： 
=2π=2π，
则曲线CDEF的长是： + +2π=4π，
所以答案是：4π．
【考点精析】通过灵活运用等边三角形的性质和弧长计算公式，掌握等边三角形的三个角都相等并且每个角都是60°；若设⊙O半径为R，n°的圆心角所对的弧长为l，则l=nπr/180;注意：在应用弧长公式进行计算时，要注意公式中n的意义．n表示1°圆心角的倍数，它是不带单位的即可以解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】⑴ 阅读理解：我们知道在直角三角形中，有无数组勾股数，例如：5、12、13；9、40、41；……但其中也有一些特殊的勾股数，例如：3、4、5；是三个连续正整数组成的勾股数.
解决问题：① 在无数组勾股数中，是否存在三个连续偶数能组成勾股数？
答： ，若存在，试写出一组勾股数： .
② 在无数组勾股数中，是否还存在其它的三个连续正整数能组成勾股数？若存在，求出勾股数，若不存在，说明理由.
③ 在无数组勾股数中，是否存在三个连续奇数能组成勾股数？若存在，求出勾股数，若不存在，说明理由.
⑵ 探索升华：是否存在锐角△ABC三边也为连续正整数；且同时还满足：∠B＞∠C＞∠A；∠ABC＝2∠BAC？若存在，求出△ABC三边的长；若不存在，说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题是真命题的是( )
A. 若a2=b2，则a=b B. 若∠1+∠2=90，则∠1与∠2互余
C. 若∠α与∠β是同位角，则∠α=∠β D. 若a⊥b，b⊥c，则a⊥c
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△OAC和△BAD都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数y=
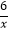在第一象限的图象经过点B，则△OAC与△BAD的面积之差S△OAC﹣S△BAD为（ ）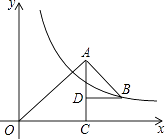 
A.36
B.12
C.6
D.3 -
科目： 来源： 题型：
查看答案和解析>>【题目】某施工工地安放了一个圆柱形饮水桶的木制支架（如图1），若不计木条的厚度，其俯视图如图2所示，已知AD垂直平分BC，AD=BC=48cm，则圆柱形饮水桶的底面半径的最大值是cm．
-
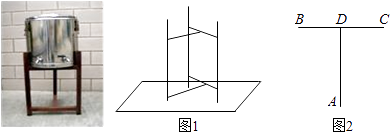
科目： 来源： 题型：
查看答案和解析>>【题目】下列几个命题:①若两个实数相等，则它们的平方相等；②若三角形的三边长a，b，c满足(a－b)(a+b)+c2=0；则这个三角形是直角三角形；③有两边和一角分别相等的两个三角形全等.其中是假命题的有_________(填序号).
-
科目： 来源： 题型：
查看答案和解析>>【题目】数学活动课上，老师提出了一个问题：
我们知道，三角形的一个外角等于和它不相邻的两个内角的和，那么三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系？
（1）独立思考，请你完成老师提出的问题：
如图所示，已知∠DBC和∠BCE分别为△ABC的两个外角，试探究∠A和∠DBC，∠BCE之间的数量关系.
解：
⑵合作交流，“创新小组”受此问题的启发：分别作外角∠CBD和∠BCE的平分线BF和CF，交于点F（如图所示），那么∠A与∠F之间有何数量关系？请写出解答过程.
相关试题
